O que é análise de regressão?
A análise de regressão estima relações ou vínculos entre uma variável dependente e uma ou mais variáveis independentes. Ela avalia a força da conexão e o potencial para relações futuras.
Ela compreende várias formas, incluindo regressão linear, múltipla linear e não linear. Os modelos mais comuns são a regressão linear simples e a múltipla linear. A regressão não linear, por outro lado, é aplicada ao lidar com conjuntos de dados complexos que apresentam uma associação não linear entre as variáveis dependentes e independentes.
Muitos profissionais preferem usar a análise de regressão para prever resultados empresariais precisos quando uma proposta de negócio depende de múltiplos fatores. A maioria dos executivos recorre a software de análise estatística para realizar essas avaliações.
Tipos de análise de regressão
A seleção da técnica e abordagem de análise de regressão depende de múltiplos fatores, como o tipo de variável dependente e o número de variáveis independentes. Abaixo estão alguns tipos comuns de análise de regressão.
- Análise de regressão linear simples é empregada para prever o valor de uma variável dependente com base no valor conhecido de uma variável independente. O método ajusta uma linha reta, permitindo definir a relação entre as duas variáveis ao estimar os coeficientes na equação linear.
- Análise de regressão múltipla descreve uma variável de resposta com a ajuda de múltiplas variáveis preditoras quando as conexões entre os dados são mais complexas. Essa abordagem funciona melhor quando fortes correlações entre as variáveis independentes podem impactar a variável dependente.
- Regressão dos mínimos quadrados ordinários é um método que estima parâmetros desconhecidos em um modelo. Calcula o coeficiente de uma equação de regressão linear ao reduzir a soma dos erros quadrados entre os valores reais e previstos que uma linha reta representa.
- Regressão polinomial, uma forma de regressão linear múltipla, entra em jogo quando a relação entre os pontos de dados é não linear. Ela determina a relação curvilínea entre variáveis independentes e dependentes.
- Regressão logística modela a probabilidade da variável dependente com base em variáveis independentes. É usada quando a variável dependente pode assumir um de um conjunto limitado de valores binários (0 e 1), tornando-a adequada para análise de dados binários.
- Regressão Bayesiana é aplicada quando os conjuntos de dados são limitados ou mal distribuídos. Quando os dados não estão disponíveis, ela usa uma distribuição de probabilidade para derivar o resultado em vez de estimativas pontuais.
- Regressão quantílica estima percentis ou quantis específicos de uma variável de resposta em vez de focar apenas na média condicional, como na regressão linear. Ela resiste à influência de outliers e não depende de suposições.
- Regressão ridge é uma técnica de regularização que mitiga a multicolinearidade entre variáveis independentes ou quando o número de variáveis independentes supera o número de observações. A multicolinearidade é um conceito estatístico em que várias variáveis independentes em um modelo são correlacionadas.
Benefícios da análise de regressão
Utilizar a análise de regressão para avaliar o impacto da mudança de variáveis oferece várias vantagens para as empresas.
- Tomada de decisões baseada em dados. Ao planejar para o futuro, as empresas confiam na análise de regressão para determinar quais variáveis influenciam significativamente os resultados.
- Reconhecendo oportunidades de melhoria. As empresas podem observar como o aumento do número de pessoas em um projeto afeta o crescimento da receita. A análise de regressão revela relações entre variáveis, capacitando as empresas a identificar oportunidades de melhoria.
- Otimização de processos empresariais. As empresas usam a análise de regressão para melhorar a eficiência operacional. Por exemplo, realizar pesquisas de consumidores antes de lançar uma nova linha de produtos ajuda a entender como vários fatores impactam a produção.
Como conduzir uma análise de regressão
Conduzir uma regressão linear envolve várias etapas-chave para calcular a relação entre uma variável dependente e uma ou mais variáveis independentes.
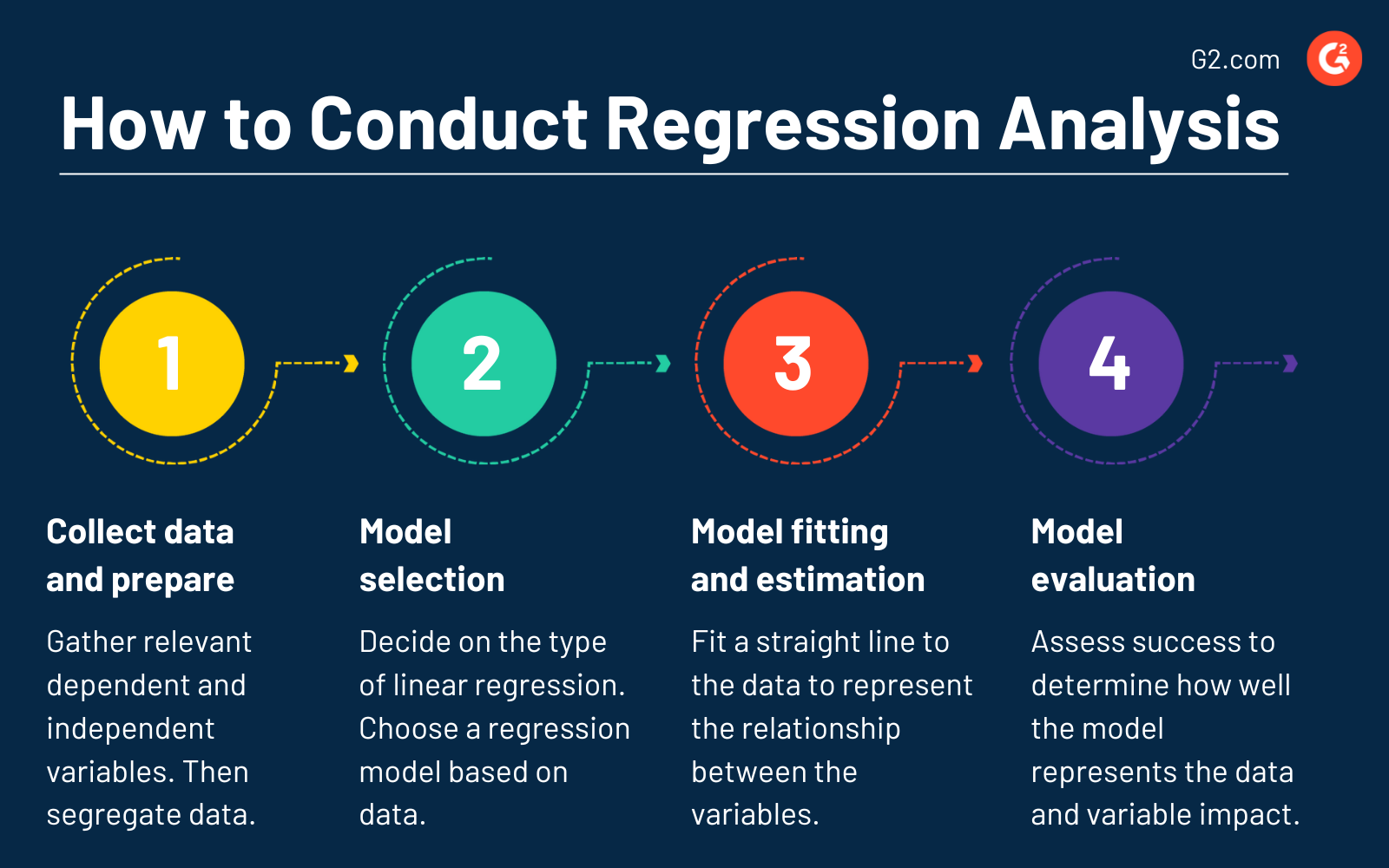
Aqui estão os principais pontos a seguir:
- Coleta e preparação de dados. Reúna variáveis dependentes e independentes relevantes. Certifique-se de que não haja valores ausentes e verifique a presença de outliers que possam impactar os resultados da análise. Separe os dados em conjuntos de treinamento e teste para avaliar o desempenho do modelo.
- Seleção do modelo. Decida o tipo de regressão linear. Escolha o modelo de regressão apropriado com base nas características dos dados.
- Ajuste do modelo e estimativa de coeficientes. Na regressão linear simples, ajuste uma linha reta aos dados que melhor representa a relação entre as variáveis dependentes e independentes. Por outro lado, estime os coeficientes da equação linear para determinar a influência das variáveis independentes sobre as variáveis dependentes na regressão linear múltipla.
- Avaliação do modelo. Avalie o sucesso para determinar quão bem o modelo representa os dados. Analise a significância dos coeficientes de regressão para entender o impacto de cada variável independente sobre a variável dependente.
Melhores práticas de análise de regressão
Abaixo estão algumas práticas essenciais para garantir que as previsões e resultados estejam próximos dos reais.
- Mantenha os conjuntos de testes atualizados. Certifique-se de verificar a funcionalidade de recursos antigos com novas atualizações.
- Utilize frameworks de teste de regressão. Empregue frameworks de teste de regressão para agilizar os esforços de manutenção.
- Adapte os designs de teste. Isso deve ser determinado pelas necessidades dos desenvolvedores e testadores.
- Implemente testes de regressão automatizados. Economize recursos e acelere a entrega por meio de testes de regressão automatizados.
- Identifique bugs antes da implantação. Testes de regressão automatizados ajudam a detectar bugs antes do prazo de implantação.
- Escale com infraestrutura de teste baseada em nuvem. À medida que as aplicações se tornam complexas, confirme que a infraestrutura de teste pode escalar para acomodar números crescentes.
Análise de regressão vs. análise de correlação
Análise de regressão é uma técnica de modelagem preditiva usada para examinar a relação entre uma variável alvo e variáveis independentes em um conjunto de dados. Várias técnicas de análise de regressão são empregadas com base em se a relação entre a variável alvo e as variáveis independentes é linear ou não linear e quando a variável alvo é composta por valores contínuos.
Análise de correlação mede a relação entre duas variáveis em vez de avaliar como duas variáveis numéricas afetam uma à outra.
Saiba mais sobre a diferença entre regressão e correlação e entenda quando usar cada uma.

Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.


















