Todos nós já ouvimos a frase "correlação não implica causalidade", mas o que isso realmente significa?
Tudo se resume a correlação vs. regressão, medidas de análise estatística usadas para encontrar conexões entre duas variáveis, medir as conexões e fazer previsões. Software de análise estatística capacita as empresas a realizar esses processos complexos por meio da importação, preparação e modelagem estatística de dados.
Investigar a relação entre duas variáveis requer conhecer as diferenças e semelhanças entre correlação e regressão. É comum haver confusão entre esses dois termos, já que a correlação pode muitas vezes levar à regressão. No entanto, há uma diferença fundamental.
Qual é a diferença entre correlação e regressão?
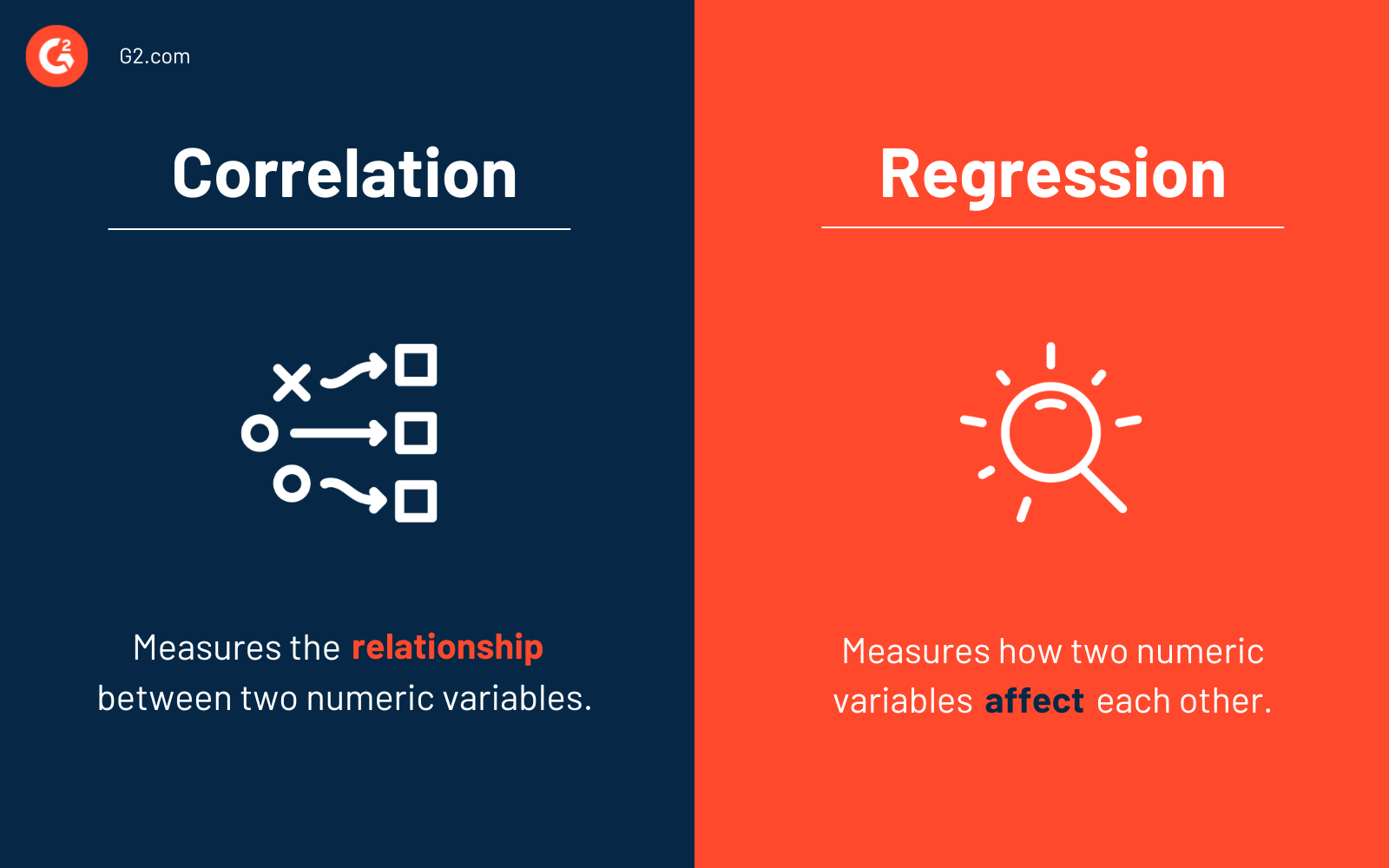
A principal diferença entre correlação e regressão é que a correlação mede o grau de relacionamento entre duas variáveis independentes (x e y). Em contraste, a regressão mostra como uma variável afeta outra.
Essencialmente, você deve saber quando usar correlação vs regressão. Use correlação para resumir a força e o grau do relacionamento entre duas ou mais variáveis numéricas. Use regressão quando você estiver procurando prever, otimizar ou explicar uma resposta numérica entre as variáveis (como x influencia y).
Correlação vs. regressão: Visão geral
Medir correlação e regressão é comum para empresas, mas também é visto em nossas vidas diárias. Por exemplo, você já viu alguém dirigindo um carro caro e automaticamente pensou que o motorista deve ser financeiramente bem-sucedido? Ou que quanto mais você corre no seu treino matinal, mais peso você perderá?
Ambos são exemplos de correlação e regressão na vida real, pois você vê uma variável (um carro luxuoso ou um treino longo) e depois verifica se há alguma relação direta com outra variável (ser rico ou perder peso).
| Correlação | Regressão | |
| Quando usar | Ao resumir a relação direta entre duas variáveis | Para prever ou explicar a resposta numérica |
| Capaz de quantificar a direção do relacionamento? | Sim | Sim |
| Capaz de quantificar a força do relacionamento? | Sim | Sim |
| Capaz de mostrar causa e efeito? | Não | Sim |
| Capaz de prever e otimizar? | Não | Sim |
| X e Y são intercambiáveis? | Sim | Não |
| Usa uma equação matemática? | Não | y = a + b (x) |
Independentemente do que você está usando correlação e regressão para ver, utilizar uma plataforma de inteligência de negócios é a melhor maneira de analisar os dados que você está observando de uma forma que seja fácil identificar quais insights acionáveis tomar. Minerar seus dados com software de inteligência de negócios permite um exame simples de big data, dados em tempo real e dados não estruturados e determina áreas para melhoria e outras tendências notáveis.
Se você não está procurando por inteligência de negócios ou plataformas de análise mas ainda espera calcular correlação e regressão, você pode encontrar ambos usando várias fórmulas do Excel. Lembre-se de que uma plataforma de BI é sua melhor aposta para maior eficiência e precisão.
Quer aprender mais sobre Software de Análise Estatística? Explore os produtos de Análise Estatística.
O que é correlação?
Para definir correlação de forma simples, pense nisso como a combinação das palavras "co" significando juntos, e "relação" significando uma conexão entre duas quantidades.
Nesse sentido, correlação é quando uma mudança segue uma mudança em uma variável em outra, seja direta ou indiretamente. As variáveis são consideradas "não correlacionadas" quando uma mudança em uma não afeta a outra. Em resumo, mede o relacionamento entre duas variáveis.
O que é correlação linear?
Dependendo da forma de uma correlação, ela pode ser de três tipos.
- Correlação linear: Quando duas variáveis mudam a uma taxa constante, ou seja, o gráfico de seu relacionamento deve ser uma linha reta.
- Correlação não linear: Quando duas variáveis não mudam a uma taxa constante. O gráfico de relacionamento será uma curva (parábolas ou hipérboles).
- Correlação monotônica: Quando duas variáveis se movem na mesma direção relativa, mas não a uma taxa constante.
Por exemplo, digamos que nossas duas variáveis sejam x e y. O tipo de correlação entre essas duas variáveis pode ser considerado positivo ou negativo. Uma mudança positiva seria quando duas variáveis se movem na mesma direção, significando que um aumento em uma variável causará um aumento em outra. Assim, se um aumento em x aumenta y, é positivamente correlacionado.
Um exemplo disso seria demanda e preço. Um aumento na demanda causa um aumento no preço. O preço aumenta porque há mais consumidores que o desejam e estão dispostos a pagar mais por ele.
Suponha que duas variáveis estejam se movendo em direções opostas, como quando um aumento em uma variável resulta em uma diminuição em outra. Isso é conhecido como correlação negativa. Um exemplo de correlação negativa é o preço e a demanda por dois produtos, pois um aumento no preço (x) resulta em uma diminuição na demanda (y).
Saber como duas variáveis estão correlacionadas permite prever tendências no futuro, pois você será capaz de entender o relacionamento entre as variáveis — ou se não há relacionamento algum.
Coeficiente de correlação
A correlação mostra como as variáveis estão relacionadas. O coeficiente de correlação (de -1 a 1) quantifica esse relacionamento. Um valor de 1 indica uma correlação positiva perfeita (ambas as variáveis se movem na mesma direção), 0 significa nenhuma correlação, e -1 indica uma correlação negativa perfeita (as variáveis se movem em direções opostas).
Análise de correlação
O principal objetivo da correlação, através da lente da análise de correlação, é permitir que os experimentadores conheçam a associação ou a ausência de um relacionamento entre duas variáveis. Quando essas variáveis estão correlacionadas, você poderá medir a força de sua associação.
No geral, a análise de correlação visa encontrar o valor numérico que mostra o relacionamento entre as duas variáveis e como elas se movem juntas.
Um benefício chave da correlação é que ela é um resumo mais conciso e claro do relacionamento entre as duas variáveis do que você encontrará com a regressão.
Fórmula de correlação
A fórmula para o coeficiente de correlação de Pearson (r), a medida de correlação mais comumente usada, é:
r = ∑(xi - x̄) (yi - ȳ) / √ [∑(xi - x̄)² * ∑(yi - ȳ)²]
onde,
- xi é o i-ésimo valor da variável x
- yi é o i-ésimo valor da variável y
- x̄ é a média da variável x
- ȳ é a média da variável y
Exemplos de correlação
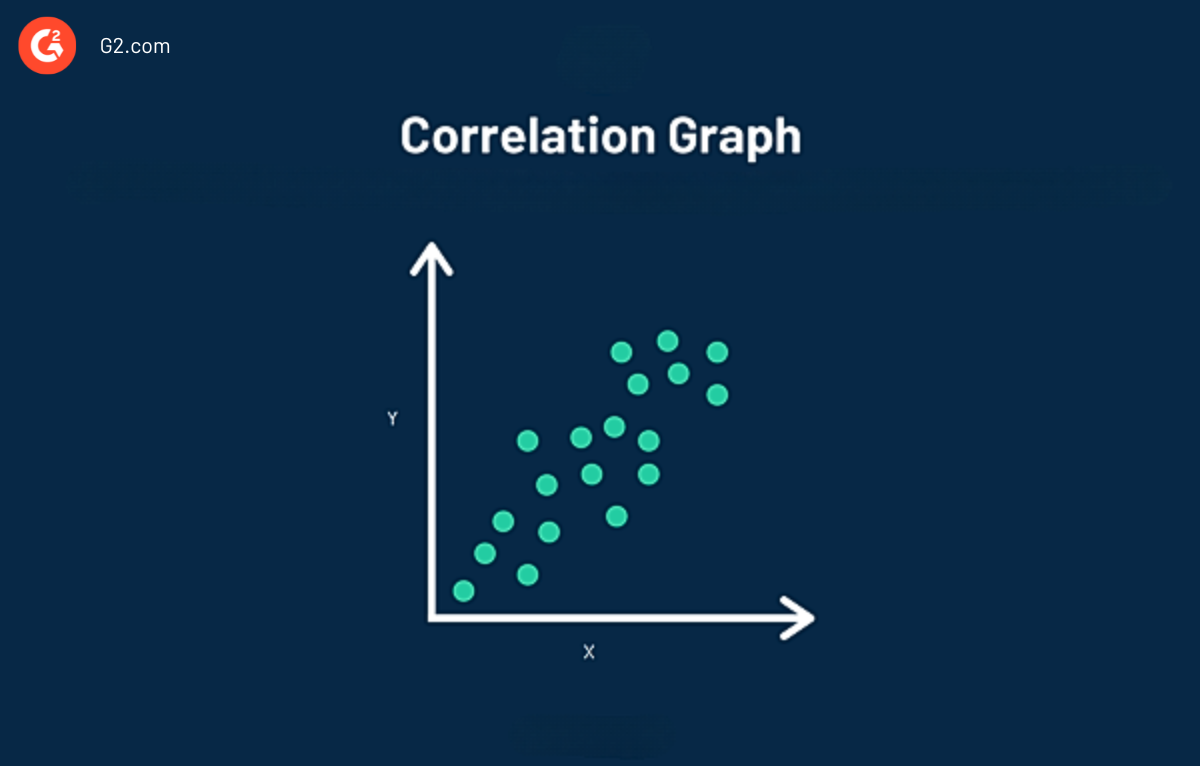
Um gráfico de correlação, também conhecido como diagrama de dispersão, facilita a visualização da correlação entre duas variáveis. Os dados em um gráfico de correlação são representados por um único ponto. No gráfico acima, você pode observar que a correlação plota vários pontos de dados únicos.
Vamos pensar na correlação como cenários da vida real. Além do exemplo de preço e demanda acima, de uma perspectiva financeira, quanto mais tempo você investir, mais juros compostos você ganhará. Ou, contratar mais vendedores resulta em maior receita devido à empresa fazer mais vendas.
Agora vamos olhar para a correlação de um ponto de vista de marketing para ver a força de um relacionamento entre duas variáveis. Por exemplo, pode ser do interesse da sua empresa ver se há uma relação previsível entre a venda de um produto e fatores como clima, publicidade e renda do consumidor.
O que é regressão?
Por outro lado, a regressão é como uma variável afeta outra ou mudanças em uma variável que desencadeiam mudanças em outra, essencialmente causa e efeito. Isso implica que o resultado depende de uma ou mais variáveis.
Por exemplo, enquanto a correlação pode ser definida como o relacionamento entre duas variáveis, a regressão é como elas afetam uma à outra. Um exemplo disso seria como um aumento na chuva causaria o crescimento de várias culturas, assim como uma seca faria com que as culturas murchassem ou não crescessem.
Quando a variável dependente aumenta enquanto a variável independente diminui, ou vice-versa, é chamada de regressão negativa. Isso contrasta com uma regressão positiva, onde ambas as variáveis dependente e independente aumentam juntas.
Coeficiente de regressão
A análise de regressão modela o relacionamento entre uma variável dependente (o resultado) e uma ou mais variáveis independentes (preditores). O coeficiente de regressão, ou inclinação, quantifica quanto a variável dependente muda para cada mudança de uma unidade em uma variável independente.
Análise de regressão
A análise de regressão ajuda a determinar a relação funcional entre duas variáveis (x e y) para que você possa estimar a variável desconhecida e fazer projeções futuras sobre eventos e metas.
O principal objetivo da análise de regressão é estimar os valores de uma variável aleatória (z) com base nos valores de suas variáveis conhecidas (ou fixas) (x e y). A análise de regressão linear é considerada a linha de melhor ajuste através dos pontos de dados.
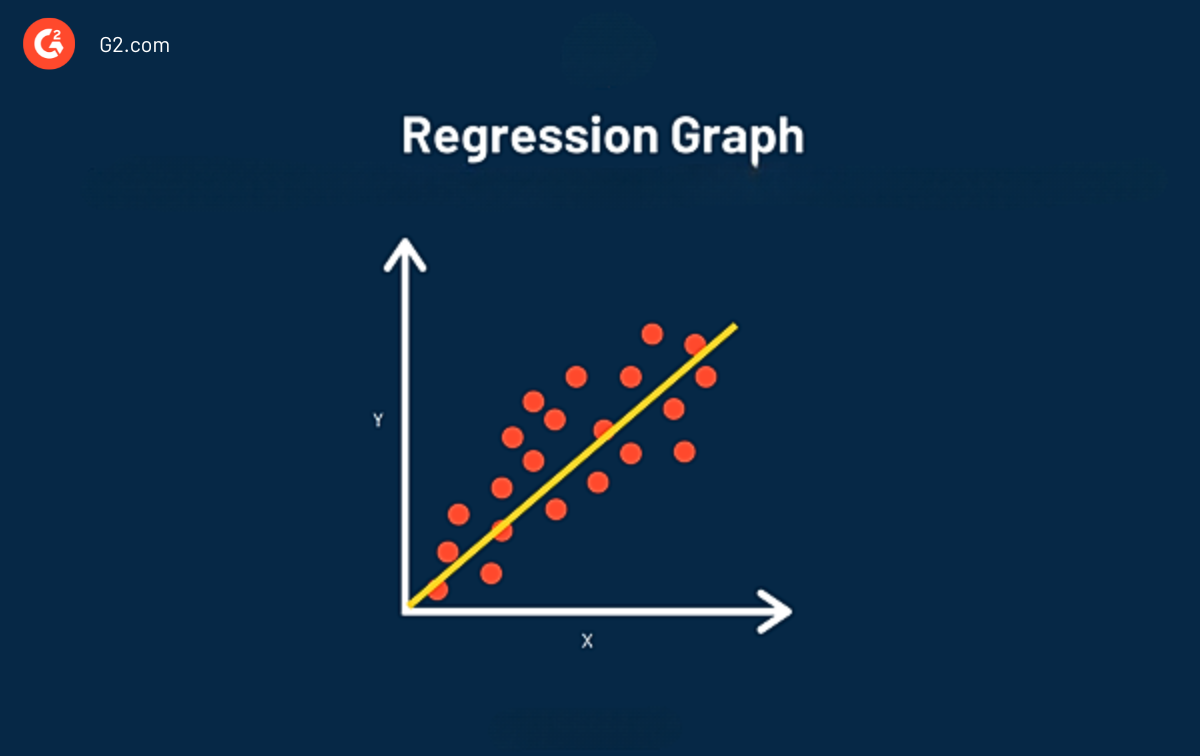
A principal vantagem de usar regressão em sua análise é que ela fornece um olhar detalhado sobre seus dados (mais detalhado do que apenas a correlação) e inclui uma equação que pode ser usada para prever e otimizar seus dados no futuro.
Quando a linha é traçada usando regressão, podemos ver duas informações:
Fórmula de regressão
a → refere-se à interseção com o eixo y, o valor de y quando x = 0
b → refere-se à inclinação, ou subida sobre corrida
A fórmula de previsão usada para ver como os dados podem parecer no futuro é:
y = a + b (x)
Exemplos de regressão
Quando se trata de usar regressão, nós na G2 utilizamos regressão para prever certas tendências, como como nosso tráfego deve crescer nos próximos meses.
Uma pessoa que usa regressão é um SEO e Analista de Dados. Visualizar dados, analisá-los, identificar tendências e prever como os dados podem parecer no futuro é uma grande parte do trabalho deles. Muitas equipes dependem de seu trabalho para definir metas de equipe e entender como nosso tráfego pode parecer no futuro.
Eles também usam as previsões de modelos baseados em regressão para definir metas para métricas importantes da empresa, como aquisição de palavras-chave. Como as previsões são baseadas em dados históricos, isso dá à empresa insights sobre como ela está atualmente em tendência em comparação com tendências de crescimento passadas.
Diferença entre correlação e regressão
Existem algumas diferenças chave entre correlação e regressão que são importantes para entender os dois.
- Fatores intercambiáveis: A regressão estabelece como x causa y a mudar, e os resultados mudarão se x e y forem trocados. Com a correlação, x e y são variáveis que podem ser trocadas e obter o mesmo resultado.
- Ponto de dados único vs. equação: A correlação é uma única estatística, ou ponto de dados, enquanto a regressão é a equação inteira com todos os pontos de dados que são representados com uma linha.
- Relacionamento vs. efeito: A correlação mostra o relacionamento entre as duas variáveis, enquanto a regressão nos permite ver como uma afeta a outra.
- Causa e efeito: Os dados mostrados com regressão estabelecem uma causa e efeito. Quando um muda, o outro também muda, e nem sempre na mesma direção. Com a correlação, as variáveis se movem juntas.
Agora é a hora de obter notícias e entretenimento SaaS-y com nosso boletim informativo de 5 minutos, G2 Tea, apresentando líderes inspiradores, opiniões ousadas e previsões audaciosas. Inscreva-se abaixo!
Semelhanças entre correlação e regressão
Além das diferenças, existem algumas semelhanças chave entre correlação e regressão que podem ajudá-lo a entender melhor seus dados.
- Ambos trabalham para quantificar a direção e a força do relacionamento entre duas variáveis numéricas.
- Qualquer momento em que a correlação é negativa, a inclinação da regressão (linha dentro do gráfico) também será negativa.
- Qualquer momento em que a correlação é positiva, a inclinação da regressão (linha dentro do gráfico) será positiva.
Perguntas frequentes sobre correlação e regressão
P. O que são regressão e correlação em estatística?
Correlação e regressão são técnicas usadas para analisar o relacionamento entre duas variáveis quantitativas. Enquanto a correlação mede a força de um relacionamento linear entre duas variáveis, a regressão em estatística mede como essas variáveis afetam uma à outra usando uma equação.
P. Qual é uma diferença chave entre regressão e correlação?
A correlação determina a conexão ou relacionamento entre duas variáveis numéricas. A regressão foca em como esse relacionamento impactará cada uma das variáveis ao longo do tempo.
P. Devo usar correlação ou regressão?
Use correlação para saber o grau de um relacionamento entre duas variáveis. Mas se você quiser analisar o efeito de como uma variável independente está numericamente associada à variável dependente, use regressão.
P. Você pode fazer correlação e regressão juntas?
Sim, a análise de correlação e regressão pode ser conduzida juntas para medir um conjunto de dados e entender o relacionamento entre variáveis.
É mais do que causa e efeito.
Embora sejam estudados juntos, é claro que há diferenças e semelhanças óbvias entre correlação e regressão.
Quando você está procurando construir um modelo, uma equação ou prever uma resposta chave, use regressão. Se você está procurando resumir rapidamente a direção e a força de um relacionamento, a correlação é sua melhor aposta.
Para conceitualizar ainda mais seus dados, use software de visualização de dados e acompanhe suas métricas de negócios e KPIs em tempo real.
Este artigo foi publicado originalmente em 2020. Foi atualizado com novas informações.

Mara Calvello
Mara Calvello is a Content and Communications Manager at G2. She received her Bachelor of Arts degree from Elmhurst College (now Elmhurst University). Mara writes content highlighting G2 newsroom events and customer marketing case studies, while also focusing on social media and communications for G2. She previously wrote content to support our G2 Tea newsletter, as well as categories on artificial intelligence, natural language understanding (NLU), AI code generation, synthetic data, and more. In her spare time, she's out exploring with her rescue dog Zeke or enjoying a good book.

