Qu'est-ce que la modélisation statistique ? Quand et où l'utiliser

Vous pouvez interpréter les données de plusieurs manières.

Cela vous aide à comprendre les ensembles de données et à créer des rapports tout en appliquant plusieurs modèles statistiques pour faire des prévisions.

Les modèles statistiques sont une représentation mathématique des données observées qui aident les analystes et les data scientists à visualiser les relations et les schémas entre les ensembles de données. De plus, ils leur fournissent une base solide pour prévoir et projeter les données pour l'avenir prévisible.

En termes simples, les modèles sont des relations entre deux variables. Par exemple, le terme « modéliser le poids et la taille de la souris » signifie établir une relation entre eux. Avec la taille, le poids augmente également. Appliquer la modélisation statistique dans cet exemple vous permet de comprendre la relation entre la taille et le poids, vous aidant à mieux analyser les ensembles de données.

Ceci est un exemple simple. Les entreprises utilisent des logiciels d'analyse statistique pour effectuer des modélisations statistiques complexes.

La modélisation statistique aide à projeter les données afin que les non-analystes et autres parties prenantes puissent baser leurs décisions dessus. Dans la modélisation statistique, les data scientists recherchent des schémas. Ils utilisent ces schémas comme échantillon et font des prédictions sur l'ensemble complet.

Lorsque vous mettez en œuvre des modèles statistiques, commencez à identifier les meilleurs modèles qui correspondent à votre objectif. Adopter ces modèles vous permettrait d'effectuer des analyses et de générer de meilleures visualisations de données.

Objectif de la modélisation statistique

Les modèles statistiques aident à comprendre les caractéristiques des données connues et à estimer les propriétés de grandes populations sur cette base. C'est l'idée centrale derrière l'apprentissage automatique.

Il vous permet de trouver une barre d'erreur ou un intervalle de confiance basé sur la taille de l'échantillon et d'autres facteurs. Par exemple, une estimation X calculée à partir de 10 échantillons aurait un intervalle de confiance plus large qu'une estimation Y calculée à partir de 10 000 échantillons.

La modélisation statistique soutient également les tests d'hypothèses. Elle fournit des preuves statistiques de la survenue d'événements spécifiques.

Où sont utilisés les modèles statistiques ?

Les modèles statistiques sont utilisés en science des données, apprentissage automatique, ingénierie ou recherche opérationnelle. Ces modèles ont diverses applications dans le monde réel.

• Modélisation spatiale fonctionne avec un système d'information géographique (SIG) et établit une relation entre les processus et les propriétés dans un espace géographique. Cela aide les chercheurs à comprendre et à prédire les phénomènes du monde réel et à planifier efficacement.
• Analyse de survie observe la durée pendant laquelle une série d'événements se produit. Selon le domaine d'étude, l'analyse de survie est également connue sous le nom d'analyse de fiabilité, modélisation de durée ou analyse de l'historique des événements. Ces modèles sont utilisés pour prédire le temps jusqu'à l'événement (TTE). Par exemple, l'analyse de survie répond à des questions telles que combien de temps il faut pour tirer la première balle après l'achat d'une arme à feu.
• Analyse de séries temporelles implique l'étude d'une série de points de données qui se produisent successivement au fil du temps. Elle fournit des informations sur les facteurs qui influencent certains événements de temps en temps.
• Systèmes de recommandation prédisent le choix ou la préférence d'un utilisateur pour un article et les notes qu'il est susceptible de donner.
• Segmentation de marché crée différents fragments de marché en fonction des besoins, préférences et priorités des acheteurs potentiels. La modélisation statistique aide les marketeurs à identifier les segments de marché pertinents pour mieux positionner leurs produits et se concentrer sur les groupes cibles.
• Apprentissage des règles d'association permet la découverte de relations intéressantes entre les variables dans de grandes bases de données. Il est utilisé dans la détection des menaces, où les règles d'association permettent aux spécialistes de la cybersécurité de détecter les fraudes.
• Modélisation prédictive aide les chercheurs à prédire les résultats ou les conséquences d'un événement, peu importe quand il se produit. Ces modèles sont souvent utilisés pour prédire la météo ou les prix du marché boursier, détecter les crimes et identifier les suspects.
• Modèles de scoring sont basés sur la régression logistique et les arbres de décision. Les enquêteurs les utilisent en combinaison avec plusieurs algorithmes pour détecter la fraude par carte de crédit.
• Clustering, ou un modèle de cluster, regroupe des éléments dans un cluster de sorte qu'il y ait plus de similitudes au sein du groupe que d'autres éléments à travers différents groupes.

Modélisation statistique vs modélisation mathématique

Bien que la modélisation statistique et mathématique aide les professionnels à comprendre les relations entre les ensembles de données, elles ne sont pas les mêmes.

La modélisation mathématique implique de transformer des problèmes du monde réel en modèles mathématiques que vous pouvez analyser pour obtenir des informations. Elle utilise des modèles statiques formulés à partir de situations réelles, ce qui la rend moins flexible.

En revanche, les modèles statistiques aidés par l'apprentissage automatique sont comparativement plus flexibles pour inclure de nouveaux schémas et tendances.

Modélisation statistique vs apprentissage automatique

La modélisation statistique et l'apprentissage automatique ne sont pas les mêmes. L'apprentissage automatique (ML) implique le développement d'algorithmes informatiques pour transformer les données en actions intelligentes, et il ne repose pas sur la programmation basée sur des règles.

Avant de faire confiance à un résultat de l'analyse statistique, toutes les hypothèses doivent être satisfaites. Cela rend la tolérance à l'incertitude faible. Contrairement à l'analyse statistique, les concepts d'apprentissage automatique ne reposent pas sur des hypothèses. Les modèles ML sont plus flexibles.

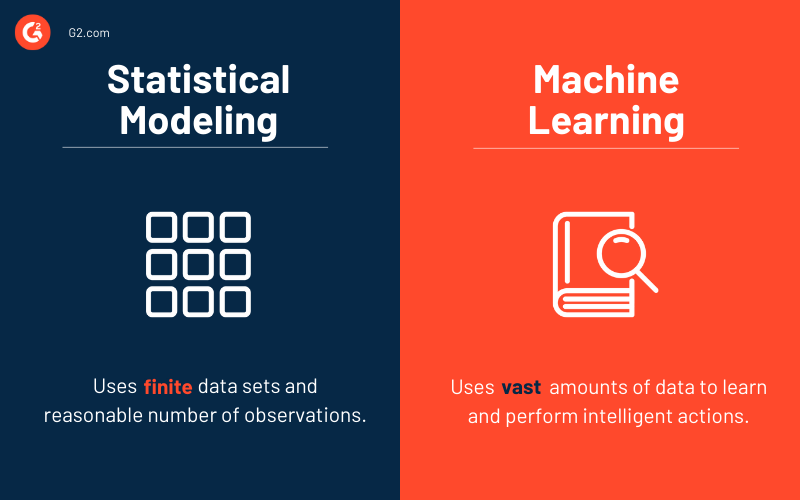
De plus, les modèles statistiques fonctionnent avec des ensembles de données finis et un nombre raisonnable d'observations. Augmenter les données pourrait conduire à un surajustement (lorsque les modèles statistiques s'ajustent à leurs données d'entraînement). Au contraire, les modèles d'apprentissage automatique ont besoin de vastes quantités de données pour apprendre et effectuer des actions intelligentes.

Quand devriez-vous utiliser la modélisation statistique ?

Vous pouvez utiliser des modèles statistiques lorsque la plupart des hypothèses sont satisfaites lors de la construction du modèle et que l'incertitude est faible.

Par exemple, lorsqu'une agence de marketing de contenu souhaite construire un modèle pour suivre le parcours d'un public, elle préférera probablement un modèle statistique avec 8 à 10 prédicteurs. Ici, le besoin d'interprétabilité est plus élevé que la précision des prédictions car cela les aiderait à développer une stratégie d'engagement basée sur la connaissance du domaine commercial.

Quand devriez-vous utiliser l'apprentissage automatique ?

Les modèles d'apprentissage automatique sont utilisés pour analyser un grand volume de données, et le résultat prédit n'a pas de composante aléatoire. Par exemple, dans la reconnaissance de motifs visuels, un objet doit être un 'E', pas un 'E'.

Par exemple, lorsque des sites de commerce électronique tels qu'Amazon souhaitent recommander des produits en fonction des achats précédents, ils ont besoin d'un moteur de recommandation puissant. Ici, le besoin de précision prédictive est plus important que l'interprétabilité du modèle, ce qui rend le modèle d'apprentissage automatique un choix approprié.

Techniques de modélisation statistique

Les données sont au cœur de la création d'un modèle statistique. Vous pouvez obtenir ces données à partir d'une feuille de calcul, d'un entrepôt de données ou d'un lac de données. La connaissance de la structure et de la gestion des données vous aiderait à récupérer les données sans problème. Vous pouvez ensuite les analyser en utilisant des méthodes d'analyse de données statistiques courantes catégorisées comme apprentissage supervisé et apprentissage non supervisé.

Les techniques d'apprentissage supervisé incluent :

• Un modèle de régression : Utilisé pour analyser la relation entre une variable dépendante et une variable indépendante. C'est un modèle statistique prédictif courant que les analystes utilisent dans la prévision, la modélisation de séries temporelles et l'identification des relations de cause à effet entre les variables. Il peut y avoir différents types de modèles de régression, tels que la régression linéaire simple et la régression linéaire multiple.
• Un modèle de classification : Un algorithme qui analyse des ensembles de données existants, grands et complexes pour les comprendre et les classer en conséquence. C'est un modèle d'apprentissage automatique qui inclut les arbres de décision, le plus proche voisin, la forêt aléatoire et les réseaux neuronaux utilisés dans l'intelligence artificielle.

Les entreprises peuvent également utiliser d'autres techniques telles que les méthodes de ré-échantillonnage et les méthodes basées sur les arbres dans l'analyse de données statistiques.

Les techniques d'apprentissage non supervisé incluent :

• Apprentissage par renforcement : Un concept de deep learning qui itère et entraîne l'algorithme à apprendre un processus optimal en récompensant les résultats favorables et en pénalisant les étapes qui produisent des résultats défavorables
• Clustering K-means : Assemble un nombre spécifié de points de données en clusters basés sur certaines similitudes
• Clustering hiérarchique : Aide à développer une hiérarchie multi-niveaux de clusters en créant un arbre de clusters

Comment construire des modèles statistiques

Lors de la construction d'un modèle statistique, la première étape consiste à choisir le meilleur modèle statistique en fonction de vos besoins.

Vous pouvez choisir le meilleur modèle pour votre objectif une fois que vous avez répondu à toutes les questions ci-dessus. Après avoir sélectionné le modèle statistique, vous pouvez commencer par les statistiques descriptives et les graphiques. Visualisez les données car cela vous aidera à reconnaître les erreurs, à comprendre les variables et leur comportement. Observez comment les variables liées fonctionnent ensemble en construisant des prédicteurs et voyez le résultat lorsque les ensembles de données sont combinés.

Vous devriez comprendre la relation entre les prédicteurs potentiels et leur corrélation avec les résultats. Suivez les résultats avec ou sans variables de contrôle. Vous pouvez éliminer les variables non significatives au début et garder toutes les variables impliquées dans le modèle.

Vous pouvez garder les questions de recherche principales en vérification tout en comprenant les relations existantes entre les variables, en testant et en catégorisant chaque prédicteur potentiel.

Les organisations peuvent tirer parti des logiciels de modélisation statistique pour collecter, organiser, examiner, interpréter et concevoir des données. Ce logiciel est doté de capacités de visualisation, de modélisation et de fouille de données qui aident à automatiser l'ensemble du processus.

Modéliser les ensembles de données pour prédire les tendances futures

Employez la modélisation statistique pour comprendre les relations entre les ensembles de données et comment les changements dans ceux-ci affecteraient les autres. Après avoir analysé cette relation, vous pouvez comprendre l'état actuel et faire des prévisions futures.

Avec une modélisation statistique appropriée, vous pouvez interpréter la relation entre les variables et tirer parti des informations pour prédire les variables que vous changeriez ou influenceriez pour obtenir le résultat attendu à l'avenir.

En savoir plus sur l'analyse statistique et trouvez de meilleures façons de prendre des décisions commerciales en utilisant les données actuelles.