Nous avons tous entendu dire que « la corrélation n'implique pas la causalité », mais que signifie vraiment cette expression ?
Tout se résume à la corrélation vs la régression, des mesures d'analyse statistique utilisées pour trouver des connexions entre deux variables, mesurer ces connexions et faire des prédictions. Les logiciels d'analyse statistique permettent aux entreprises de mener ces processus complexes grâce à l'importation, la préparation et la modélisation statistique des données.
Pour enquêter sur la relation entre deux variables, il est nécessaire de connaître les différences et les similitudes entre la corrélation et la régression. Il est courant de confondre ces deux termes, car la corrélation peut souvent conduire à la régression. Cependant, il y a une différence clé.
Quelle est la différence entre corrélation et régression ?
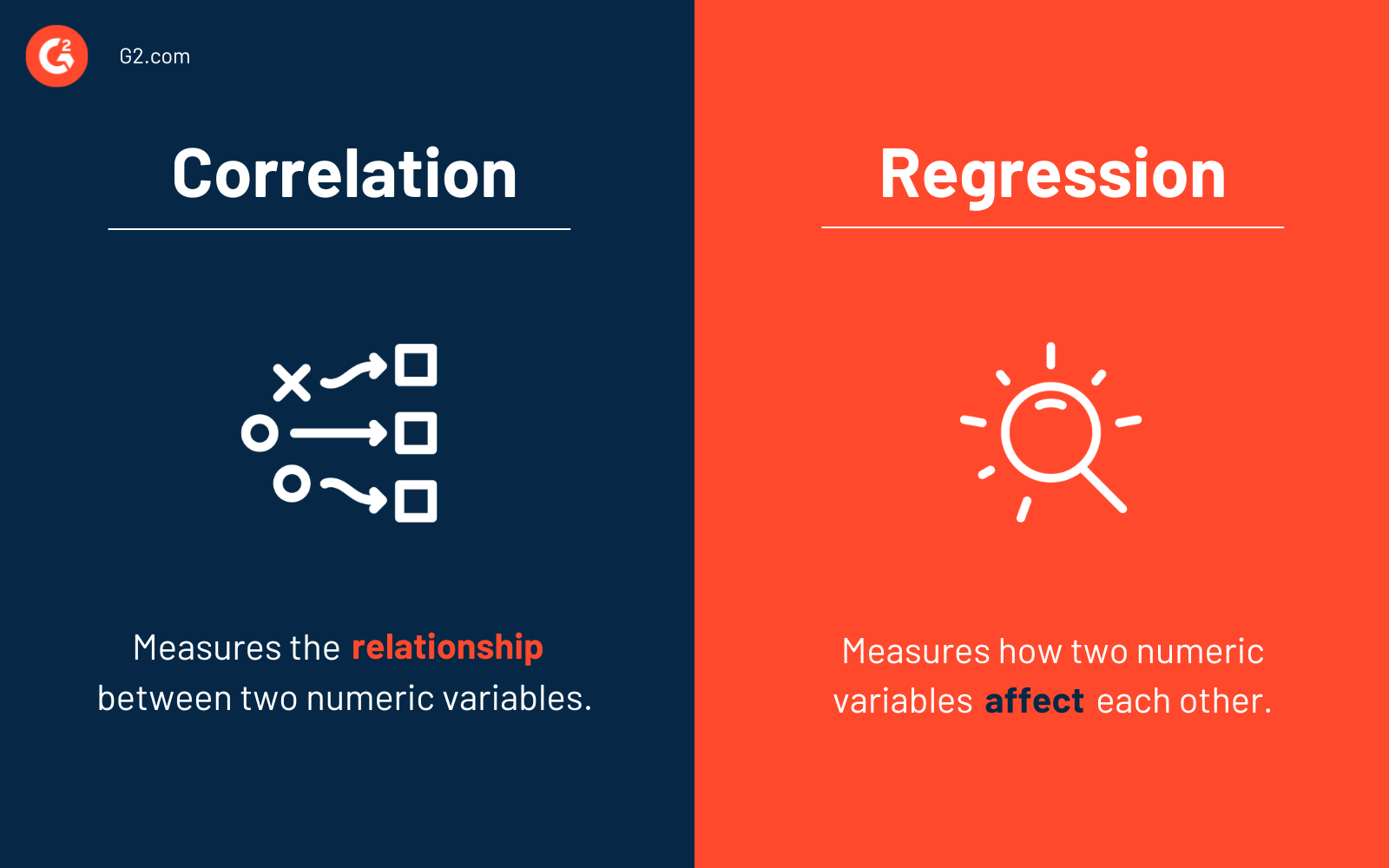
La différence clé entre la corrélation et la régression est que la corrélation mesure le degré de relation entre deux variables indépendantes (x et y). En revanche, la régression montre comment une variable affecte une autre.
Essentiellement, vous devez savoir quand utiliser la corrélation vs la régression. Utilisez la corrélation pour résumer la force et le degré de la relation entre deux ou plusieurs variables numériques. Utilisez la régression lorsque vous cherchez à prédire, optimiser ou expliquer une réponse numérique entre les variables (comment x influence y).
Corrélation vs régression : Aperçu
Mesurer la corrélation et la régression est courant pour les entreprises, mais cela se voit aussi dans notre vie quotidienne. Par exemple, avez-vous déjà vu quelqu'un conduire une voiture chère et pensé automatiquement que le conducteur devait être financièrement prospère ? Ou bien avez-vous pensé que plus vous courez lors de votre entraînement matinal, plus vous perdrez de poids ?
Ce sont deux exemples de corrélation et de régression dans la vie réelle, car vous voyez une variable (une voiture de luxe ou un long entraînement) et vérifiez ensuite s'il existe une relation directe avec une autre variable (être riche ou perdre du poids).
| Corrélation | Régression | |
| Quand l'utiliser | Pour résumer la relation directe entre deux variables | Pour prédire ou expliquer la réponse numérique |
| Capable de quantifier la direction de la relation ? | Oui | Oui |
| Capable de quantifier la force de la relation ? | Oui | Oui |
| Capable de montrer la cause et l'effet ? | Non | Oui |
| Capable de prédire et d'optimiser ? | Non | Oui |
| X et Y sont interchangeables ? | Oui | Non |
| Utilise une équation mathématique ? | Non | y = a + b (x) |
Peu importe ce que vous utilisez pour voir la corrélation et la régression, utiliser une plateforme d'intelligence d'affaires est le meilleur moyen d'analyser les données que vous examinez de manière à identifier facilement les informations exploitables à prendre. L'exploitation de vos données avec un logiciel d'intelligence d'affaires permet un examen simple des big data, des données en temps réel et des données non structurées, et détermine les domaines à améliorer et d'autres tendances notables.
Si vous ne recherchez pas d'intelligence d'affaires ou de plateformes d'analyse mais espérez toujours calculer la corrélation et la régression, vous pouvez trouver les deux en utilisant diverses formules Excel. Rappelez-vous qu'une plateforme BI est votre meilleur pari pour une efficacité et une précision accrues.
Vous voulez en savoir plus sur Logiciel d'analyse statistique ? Découvrez les produits Analyse statistique.
Qu'est-ce que la corrélation ?
Pour définir simplement la corrélation, pensez-y comme à la combinaison des mots « co » signifiant ensemble, et « relation » signifiant une connexion entre deux quantités.
Dans ce sens, la corrélation est lorsqu'un changement suit un changement d'une variable dans une autre, qu'il soit direct ou indirect. Les variables sont considérées comme « non corrélées » lorsqu'un changement dans l'une n'affecte pas l'autre. En bref, elle mesure la relation entre deux variables.
Qu'est-ce que la corrélation linéaire ?
Selon la forme d'une corrélation, elle peut être de trois types.
- Corrélation linéaire : Lorsque deux variables changent à un taux constant, c'est-à-dire que leur graphique de relation doit être une ligne droite.
- Corrélation non linéaire : Lorsque deux variables ne changent pas à un taux constant. Le graphique de la relation sera une courbe (paraboles ou hyperboles).
- Corrélation monotone : Lorsque deux variables se déplacent dans la même direction relative mais pas à un taux constant.
Par exemple, disons que nos deux variables sont x et y. Le type de corrélation entre ces deux variables peut être considéré comme positif ou négatif. Un changement positif serait lorsque deux variables se déplacent dans la même direction, ce qui signifie qu'une augmentation d'une variable entraînera une augmentation d'une autre. Donc, si une augmentation de x augmente y, elles sont positivement corrélées.
Un exemple de cela serait la demande et le prix. Une augmentation de la demande entraîne une augmentation du prix. Le prix augmente parce qu'il y a plus de consommateurs qui le veulent et sont prêts à payer plus pour cela.
Supposons que deux variables se déplacent dans des directions opposées, comme lorsqu'une augmentation d'une variable entraîne une diminution d'une autre. Cela est connu sous le nom de corrélation négative. Un exemple de corrélation négative est le prix et la demande de deux produits, car une augmentation du prix (x) entraîne une diminution de la demande (y).
Savoir comment deux variables sont corrélées permet de prédire les tendances futures, car vous serez en mesure de comprendre la relation entre les variables — ou s'il n'y a pas de relation du tout.
Coefficient de corrélation
La corrélation montre comment les variables sont liées. Le coefficient de corrélation (de -1 à 1) quantifie cette relation. Une valeur de 1 indique une corrélation positive parfaite (les deux variables se déplacent dans la même direction), 0 signifie aucune corrélation, et -1 indique une corrélation négative parfaite (les variables se déplacent dans des directions opposées).
Analyse de corrélation
Le principal objectif de la corrélation, à travers le prisme de l'analyse de corrélation, est de permettre aux expérimentateurs de connaître l'association ou l'absence de relation entre deux variables. Lorsque ces variables sont corrélées, vous pourrez mesurer la force de leur association.
Dans l'ensemble, l'analyse de corrélation vise à trouver la valeur numérique qui montre la relation entre les deux variables et comment elles se déplacent ensemble.
Un avantage clé de la corrélation est qu'elle est un résumé plus concis et clair de la relation entre les deux variables que vous ne trouverez avec la régression.
Formule de corrélation
La formule pour le coefficient de corrélation de Pearson (r), la mesure de corrélation la plus couramment utilisée, est :
r = ∑(xi - x̄) (yi - ȳ) / √ [∑(xi - x̄)² * ∑(yi - ȳ)²]
où,
- xi est la ième valeur de la variable x
- yi est la ième valeur de la variable y
- x̄ est la moyenne de la variable x
- ȳ est la moyenne de la variable y
Exemples de corrélation
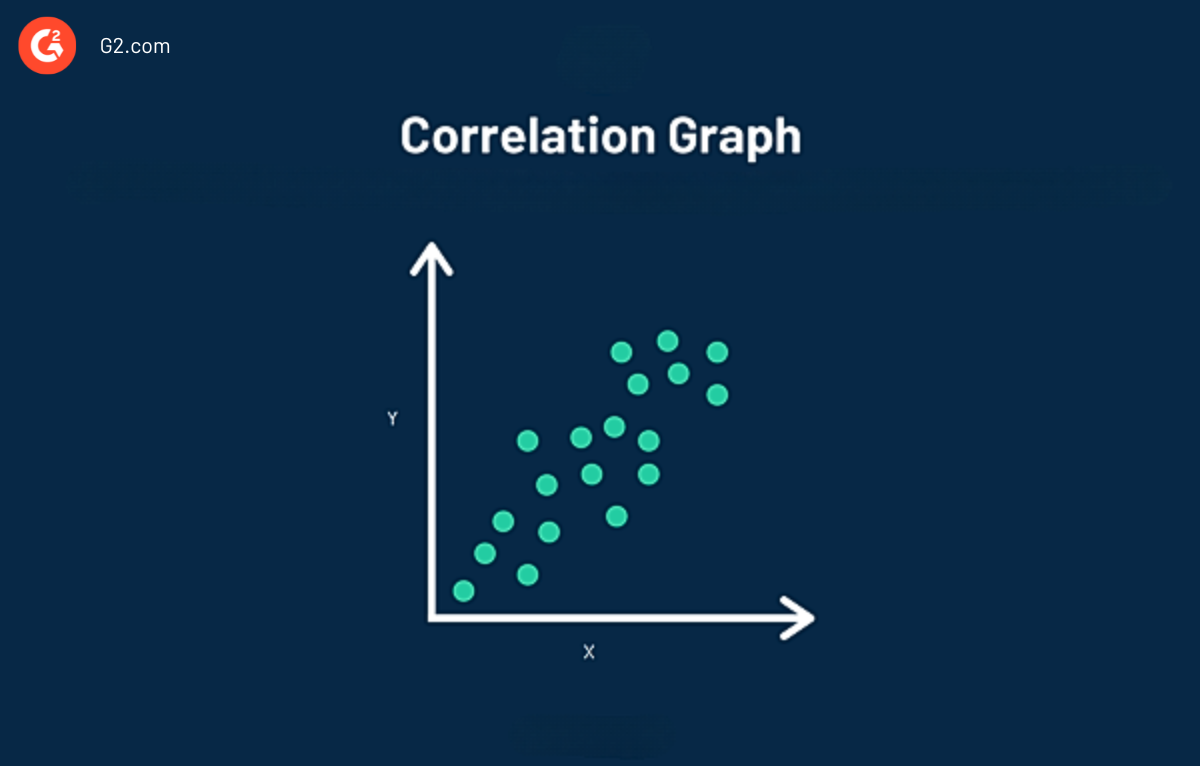
Un graphique de corrélation, également connu sous le nom de diagramme de dispersion, facilite la visualisation de la corrélation entre deux variables. Les données dans un graphique de corrélation sont représentées par un seul point. Dans le graphique ci-dessus, vous pouvez observer que la corrélation trace divers points de données uniques.
Considérons la corrélation comme des scénarios de la vie réelle. En plus de l'exemple de prix et de demande ci-dessus, d'un point de vue financier, plus vous investissez longtemps, plus vous gagnerez d'intérêts composés. Ou, embaucher plus de vendeurs entraîne une augmentation des revenus grâce à l'augmentation des ventes de l'entreprise.
Examinons maintenant la corrélation d'un point de vue marketing pour voir la force d'une relation entre deux variables. Par exemple, il pourrait être dans l'intérêt de votre entreprise de voir s'il existe une relation prévisible entre la vente d'un produit et des facteurs tels que la météo, la publicité et le revenu des consommateurs.
Qu'est-ce que la régression ?
En revanche, la régression montre comment une variable affecte une autre ou comment des changements dans une variable déclenchent des changements dans une autre, essentiellement cause et effet. Cela implique que le résultat dépend d'une ou plusieurs variables.
Par exemple, alors que la corrélation peut être définie comme la relation entre deux variables, la régression montre comment elles s'affectent mutuellement. Un exemple de cela serait comment une augmentation des précipitations entraînerait la croissance de diverses cultures, tout comme une sécheresse entraînerait le flétrissement ou la non-croissance des cultures.
Lorsque la variable dépendante augmente tandis que la variable indépendante diminue, ou vice versa, on parle de régression négative. Cela contraste avec une régression positive, où les deux variables dépendantes et indépendantes augmentent ensemble.
Coefficient de régression
L'analyse de régression modélise la relation entre une variable dépendante (le résultat) et une ou plusieurs variables indépendantes (prédicteurs). Le coefficient de régression, ou pente, quantifie combien la variable dépendante change pour chaque changement d'une unité dans une variable indépendante.
Analyse de régression
L'analyse de régression aide à déterminer la relation fonctionnelle entre deux variables (x et y) afin que vous puissiez estimer la variable inconnue et faire des projections futures sur des événements et des objectifs.
L'objectif principal de l'analyse de régression est d'estimer les valeurs d'une variable aléatoire (z) en fonction des valeurs de vos variables connues (ou fixes) (x et y). L'analyse de régression linéaire est considérée comme la meilleure ligne de tendance à travers les points de données.
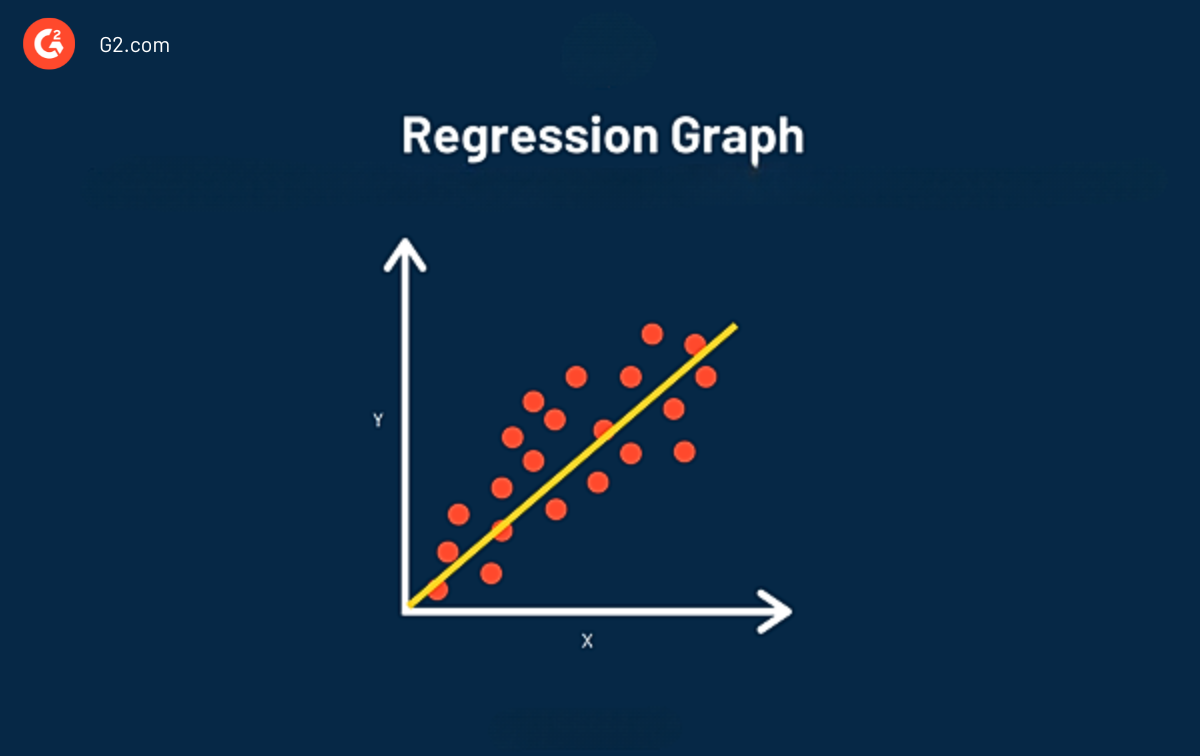
L'avantage principal d'utiliser la régression dans votre analyse est qu'elle fournit un regard détaillé sur vos données (plus détaillé que la corrélation seule) et inclut une équation qui peut être utilisée pour prédire et optimiser vos données à l'avenir.
Lorsque la ligne est tracée en utilisant la régression, nous pouvons voir deux informations :
Formule de régression
a → se réfère à l'ordonnée à l'origine, la valeur de y lorsque x = 0
b → se réfère à la pente, ou montée sur course
La formule de prédiction utilisée pour voir comment les données pourraient ressembler à l'avenir est :
y = a + b (x)
Exemples de régression
En ce qui concerne l'utilisation de la régression, nous chez G2 utilisons la régression pour prédire certaines tendances, comme comment notre trafic devrait croître au cours des prochains mois.
Une personne qui utilise la régression est un SEO et analyste de données. Visualiser les données, les analyser, identifier les tendances et prédire à quoi pourraient ressembler les données à l'avenir est une grande partie de leur travail. De nombreuses équipes comptent sur leur travail pour fixer des objectifs d'équipe et comprendre comment notre trafic pourrait ressembler à l'avenir.
Ils utilisent également les prédictions des modèles basés sur la régression pour fixer des objectifs pour des métriques importantes de l'entreprise, comme l'acquisition de mots-clés. Étant donné que les prédictions sont basées sur des données historiques, cela donne à l'entreprise des informations sur la façon dont elle évolue actuellement par rapport aux tendances de croissance passées.
Différence entre corrélation et régression
Il existe quelques différences clés entre la corrélation et la régression qui sont importantes pour comprendre les deux.
- Facteurs interchangeables : La régression établit comment x cause y à changer, et les résultats changeront si x et y sont échangés. Avec la corrélation, x et y sont des variables qui peuvent être échangées et obtenir le même résultat.
- Point de données unique vs équation : La corrélation est une statistique unique, ou un point de données, tandis que la régression est l'ensemble de l'équation avec tous les points de données représentés par une ligne.
- Relation vs effet : La corrélation montre la relation entre les deux variables, tandis que la régression nous permet de voir comment l'une affecte l'autre.
- Cause et effet : Les données montrées avec la régression établissent une cause et un effet. Lorsque l'une change, l'autre aussi, et pas toujours dans la même direction. Avec la corrélation, les variables se déplacent ensemble.
Il est maintenant temps de recevoir des nouvelles et du divertissement SaaS avec notre newsletter de 5 minutes, G2 Tea, mettant en vedette des leaders inspirants, des opinions tranchées et des prédictions audacieuses. Abonnez-vous ci-dessous !
Similitudes entre corrélation et régression
En plus des différences, il existe quelques similitudes clés entre la corrélation et la régression qui peuvent vous aider à mieux comprendre vos données.
- Les deux travaillent à quantifier la direction et la force de la relation entre deux variables numériques.
- Chaque fois que la corrélation est négative, la pente de régression (ligne dans le graphique) sera également négative.
- Chaque fois que la corrélation est positive, la pente de régression (ligne dans le graphique) sera positive.
Questions fréquemment posées sur la corrélation et la régression
Q. Qu'est-ce que la régression et la corrélation en statistiques ?
La corrélation et la régression sont des techniques utilisées pour analyser la relation entre deux variables quantitatives. Alors que la corrélation mesure la force d'une relation linéaire entre deux variables, la régression en statistiques mesure comment ces variables s'affectent mutuellement à l'aide d'une équation.
Q. Quelle est une différence clé entre la régression et la corrélation ?
La corrélation détermine la connexion ou la relation entre deux variables numériques. La régression se concentre sur la façon dont cette relation affectera chacune des variables au fil du temps.
Q. Dois-je utiliser la corrélation ou la régression ?
Utilisez la corrélation pour connaître le degré de relation entre deux variables. Mais si vous voulez analyser l'effet de la façon dont une variable indépendante est numériquement associée à la variable dépendante, utilisez la régression.
Q. Pouvez-vous faire la corrélation et la régression ensemble ?
Oui, l'analyse de corrélation et de régression peut être menée ensemble pour mesurer un ensemble de données et comprendre la relation entre les variables.
C'est plus que cause et effet.
Bien qu'elles soient étudiées ensemble, il est clair qu'il existe des différences et des similitudes évidentes entre la corrélation et la régression.
Lorsque vous cherchez à construire un modèle, une équation ou à prédire une réponse clé, utilisez la régression. Si vous cherchez à résumer rapidement la direction et la force d'une relation, la corrélation est votre meilleur pari.
Pour mieux conceptualiser vos données, utilisez un logiciel de visualisation de données et suivez vos indicateurs de performance et KPI en temps réel.
Cet article a été publié à l'origine en 2020. Il a été mis à jour avec de nouvelles informations.

Mara Calvello
Mara Calvello is a Content and Communications Manager at G2. She received her Bachelor of Arts degree from Elmhurst College (now Elmhurst University). Mara writes content highlighting G2 newsroom events and customer marketing case studies, while also focusing on social media and communications for G2. She previously wrote content to support our G2 Tea newsletter, as well as categories on artificial intelligence, natural language understanding (NLU), AI code generation, synthetic data, and more. In her spare time, she's out exploring with her rescue dog Zeke or enjoying a good book.

