Análisis de regresión

¿Qué es el análisis de regresión?

El análisis de regresión estima las relaciones o vínculos entre una variable dependiente y una o más variables independientes. Evalúa la fuerza de la conexión y el potencial para relaciones futuras. 

Comprende varias formas, incluyendo regresión lineal, regresión lineal múltiple y regresión no lineal. Los modelos más comunes son la regresión lineal simple y la regresión lineal múltiple. La regresión no lineal, por otro lado, se aplica cuando se trata de conjuntos de datos complejos que muestran una asociación no lineal entre las variables dependiente e independiente.

Muchos profesionales prefieren usar el análisis de regresión para predecir resultados empresariales precisos cuando una propuesta de negocio depende de múltiples factores. La mayoría de los ejecutivos recurren a software de análisis estadístico para realizar estas evaluaciones.

Software de Análisis de regresión

Software que menciona a análisis de regresión como una característica o término.

IBM SPSS Statistics

eviews

Minitab Statistical Software

Posit

Stata

Marketpay

Tipos de análisis de regresión

La técnica y enfoque del análisis de regresión dependen de múltiples factores, como el tipo de variable dependiente y el número de variables independientes. A continuación, se presentan algunos tipos comunes de análisis de regresión.

• Análisis de regresión lineal simple se emplea para pronosticar el valor de una variable dependiente basado en el valor conocido de una variable independiente. El método ajusta una línea recta, permitiendo definir la relación entre las dos variables al estimar los coeficientes en la ecuación lineal.
• Análisis de regresión múltiple describe una variable de respuesta con la ayuda de múltiples variables predictoras cuando las conexiones entre los datos son más intrincadas. Este enfoque funciona mejor cuando las fuertes correlaciones entre las variables independientes pueden impactar la variable dependiente.
• Regresión de mínimos cuadrados ordinarios es un método que estima parámetros desconocidos en un modelo. Calcula el coeficiente de una ecuación de regresión lineal al reducir la suma de los errores al cuadrado entre los valores reales y los valores predichos que representa una línea recta.
• Regresión polinómica, una forma de regresión lineal múltiple, entra en juego cuando la relación entre los puntos de datos es no lineal. Determina la relación curvilínea entre las variables independientes y dependientes. 
• Regresión logística modela la probabilidad de la variable dependiente basada en variables independientes. Se utiliza cuando la variable dependiente puede tomar uno de un conjunto limitado de valores binarios (0 y 1), lo que la hace adecuada para el análisis de datos binarios.
• Regresión bayesiana se aplica cuando los conjuntos de datos son limitados o están mal distribuidos. Cuando los datos no están disponibles, utiliza una distribución de probabilidad para derivar el resultado en lugar de estimaciones puntuales.
• Regresión cuantílica estima percentiles o cuantiles específicos de una variable de respuesta en lugar de centrarse únicamente en la media condicional, como en la regresión lineal. Resiste la influencia de los valores atípicos y no depende de suposiciones.
• Regresión de cresta es una técnica de regularización que mitiga la multicolinealidad entre las variables independientes o cuando el número de variables independientes supera el número de observaciones. La multicolinealidad es un concepto estadístico en el que varias variables independientes en un modelo están correlacionadas.

Beneficios del análisis de regresión

Utilizar el análisis de regresión para evaluar el impacto de cambiar variables ofrece varias ventajas para las empresas. 

• Tomar decisiones basadas en datos. Al planificar para el futuro, las empresas confían en el análisis de regresión para determinar qué variables influyen significativamente en los resultados. 
• Reconocer oportunidades de mejora. Las empresas pueden observar cómo el aumento del número de personas en un proyecto afecta el crecimiento de los ingresos. El análisis de regresión revela relaciones entre variables, empoderando a las empresas para identificar oportunidades de mejora.
• Optimizar procesos empresariales. Las empresas utilizan el análisis de regresión para mejorar la eficiencia operativa. Por ejemplo, realizar encuestas a consumidores antes de lanzar una nueva línea de productos les ayuda a entender cómo varios factores impactan la producción.

Cómo realizar un análisis de regresión

Realizar una regresión lineal implica varios pasos clave para calcular la relación entre una variable dependiente y una o más variables independientes.

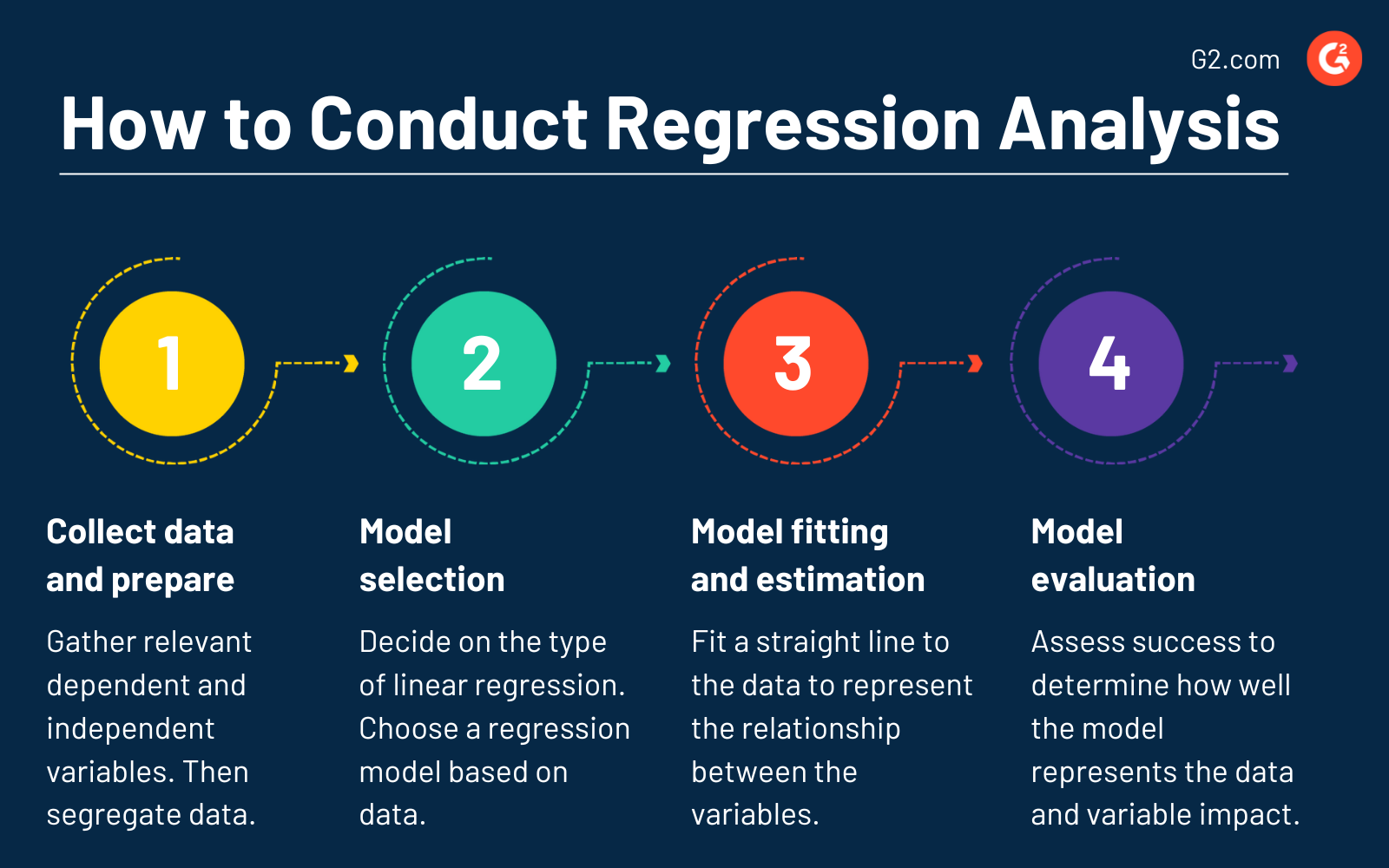
Aquí están los puntos principales a seguir:

• Recolección y preparación de datos. Reúne variables dependientes e independientes relevantes. Asegúrate de que no haya valores faltantes y verifica la presencia de valores atípicos que puedan impactar los resultados del análisis. Separa los datos en conjuntos de entrenamiento y prueba para evaluar el rendimiento del modelo.

• Selección del modelo. Decide el tipo de regresión lineal. Elige el modelo de regresión apropiado basado en las características de los datos.

• Ajuste del modelo y estimación de coeficientes. En la regresión lineal simple, ajusta una línea recta a los datos que mejor representa la relación entre las variables dependiente e independiente. Por el contrario, estima los coeficientes de la ecuación lineal para determinar la influencia de las variables independientes en las variables dependientes para la regresión lineal múltiple. 

• Evaluación del modelo. Evalúa el éxito para determinar qué tan bien el modelo representa los datos. Analiza la significancia de los coeficientes de regresión para entender el impacto de cada variable independiente en la variable dependiente.

Mejores prácticas para el análisis de regresión

A continuación, se presentan algunas prácticas esenciales para asegurar que las predicciones y resultados estén cerca de los reales.

• Mantén actualizadas las suites de prueba. Asegúrate de verificar la funcionalidad de características antiguas con nuevas actualizaciones.
• Utiliza un marco de pruebas de regresión. Emplea marcos de pruebas de regresión para agilizar los esfuerzos de mantenimiento.
• Adapta los diseños de prueba. Esto debe ser determinado por las necesidades de los desarrolladores y testers.
• Implementa pruebas de regresión automatizadas. Ahorra recursos y acelera la entrega mediante pruebas de regresión automatizadas.
• Identifica errores antes del despliegue. Las pruebas de regresión automatizadas ayudan a detectar errores antes de la fecha límite de despliegue.
• Escala con infraestructura de pruebas basada en la nube. A medida que las aplicaciones se vuelven complejas, confirma que la infraestructura de pruebas pueda escalar para acomodar números en expansión.

Análisis de regresión vs. análisis de correlación

El análisis de regresión es una técnica de modelado predictivo utilizada para examinar la relación de un conjunto de datos entre una variable objetivo y variables independientes. Se emplean varias técnicas de análisis de regresión basadas en si la relación entre la variable objetivo y las variables independientes es lineal o no lineal y cuando la variable objetivo comprende valores continuos.

El análisis de correlación mide la relación entre dos variables en lugar de evaluar cómo dos variables numéricas se afectan mutuamente.

Aprende más sobre la diferencia entre regresión y correlación y entiende cuándo usar cuál.