Todos hemos escuchado "la correlación no implica causalidad", pero ¿qué significa realmente?
Todo se reduce a correlación vs. regresión, medidas de análisis estadístico utilizadas para encontrar conexiones entre dos variables, medir las conexiones y hacer predicciones. El software de análisis estadístico permite a las empresas llevar a cabo estos procesos complejos a través de la importación, preparación y modelado estadístico de datos.
Investigar la relación entre dos variables requiere conocer las diferencias y similitudes entre correlación y regresión. Es común confundirse entre estos dos términos, ya que la correlación a menudo puede llevar a la regresión. Sin embargo, hay una diferencia clave.
¿Cuál es la diferencia entre correlación y regresión?
La diferencia clave entre correlación y regresión es que la correlación mide el grado de relación entre dos variables independientes (x e y). En cambio, la regresión es cómo una variable afecta a otra.
Esencialmente, debes saber cuándo usar correlación vs regresión. Usa correlación para resumir la fuerza y el grado de la relación entre dos o más variables numéricas. Usa regresión cuando busques predecir, optimizar o explicar una respuesta numérica entre las variables (cómo x influye en y).
Correlación vs. regresión: Resumen
Medir la correlación y la regresión es común para las empresas, pero también se ve en nuestra vida diaria. Por ejemplo, ¿alguna vez has visto a alguien conduciendo un coche caro y automáticamente pensaste que el conductor debe ser financieramente exitoso? ¿O qué tal pensar que cuanto más corres en tu entrenamiento matutino, más peso perderás?
Ambos son ejemplos de correlación y regresión en la vida real, ya que ves una variable (un coche lujoso o un entrenamiento largo) y luego verificas si hay alguna relación directa con otra variable (ser rico o perder peso).
| Correlación | Regresión | |
| Cuándo usar | Al resumir la relación directa entre dos variables | Para predecir o explicar la respuesta numérica |
| ¿Capaz de cuantificar la dirección de la relación? | Sí | Sí |
| ¿Capaz de cuantificar la fuerza de la relación? | Sí | Sí |
| ¿Capaz de mostrar causa y efecto? | No | Sí |
| ¿Capaz de predecir y optimizar? | No | Sí |
| ¿X e Y son intercambiables? | Sí | No |
| ¿Usa una ecuación matemática? | No | y = a + b (x) |
Independientemente de lo que estés usando para ver la correlación y la regresión, utilizar una plataforma de inteligencia empresarial es la mejor manera de analizar los datos que estás observando de una manera que sea fácil de identificar qué ideas accionables tomar. Minar tus datos con software de inteligencia empresarial permite un examen simple de big data, datos en tiempo real y datos no estructurados y determina áreas de mejora y otras tendencias notables.
Si no estás buscando inteligencia empresarial o plataformas de análisis pero aún esperas calcular la correlación y la regresión, puedes encontrar ambos usando varias fórmulas de Excel. Recuerda que una plataforma de BI es tu mejor opción para aumentar la eficiencia y la precisión.
¿Quieres aprender más sobre Software de Análisis Estadístico? Explora los productos de Análisis Estadístico.
¿Qué es la correlación?
Para definir simplemente la correlación, piensa en ella como la combinación de las palabras "co" que significa juntos, y "relación" que significa una conexión entre dos cantidades.
En este sentido, la correlación es cuando un cambio sigue a un cambio en una variable en otra, ya sea directa o indirectamente. Se cree que las variables están "no correlacionadas" cuando un cambio en una no afecta a la otra. En resumen, mide la relación entre dos variables.
¿Qué es la correlación lineal?
Dependiendo de la forma de una correlación, podría ser de uno de tres tipos.
- Correlación lineal: Cuando dos variables cambian a una tasa constante, es decir, su gráfico de relación debe ser una línea recta.
- Correlación no lineal: Cuando dos variables no cambian a una tasa constante. El gráfico de relación será una curva (parábolas o hipérbolas).
- Correlación monótona: Cuando dos variables se mueven en la misma dirección relativa pero no a una tasa constante.
Por ejemplo, digamos que nuestras dos variables son x e y. El tipo de correlación entre estas dos variables puede considerarse positivo o negativo. Un cambio positivo sería cuando dos variables se mueven en la misma dirección, lo que significa que un aumento en una variable causará un aumento en otra. Entonces, si un aumento en x aumenta y, está positivamente correlacionado.
Un ejemplo de esto sería la demanda y el precio. Un aumento en la demanda causa un aumento en el precio. El precio aumenta porque hay más consumidores que lo quieren y están dispuestos a pagar más por él.
Supongamos que dos variables se mueven en direcciones opuestas, como cuando un aumento en una variable resulta en una disminución en otra. Esto se conoce como una correlación negativa. Un ejemplo de una correlación negativa es el precio y la demanda de dos productos porque un aumento en el precio (x) resulta en una disminución en la demanda (y).
Saber cómo están correlacionadas dos variables permite predecir tendencias en el futuro, ya que podrás entender la relación entre las variables, o si no hay relación en absoluto.
Coeficiente de correlación
La correlación muestra cómo están relacionadas las variables. El coeficiente de correlación (de -1 a 1) cuantifica esa relación. Un valor de 1 indica una correlación positiva perfecta (ambas variables se mueven en la misma dirección), 0 significa ninguna correlación, y -1 indica una correlación negativa perfecta (las variables se mueven en direcciones opuestas).
Análisis de correlación
El propósito principal de la correlación, a través del lente del análisis de correlación, es permitir a los experimentadores conocer la asociación o la ausencia de una relación entre dos variables. Cuando estas variables están correlacionadas, podrás medir la fuerza de su asociación.
En general, el análisis de correlación tiene como objetivo encontrar el valor numérico que muestra la relación entre las dos variables y cómo se mueven juntas.
Un beneficio clave de la correlación es que es un resumen más conciso y claro de la relación entre las dos variables que el que encontrarás con la regresión.
Fórmula de correlación
La fórmula para el coeficiente de correlación de Pearson (r), la medida de correlación más utilizada, es:
r = ∑(xi - x̄) (yi - ȳ) / √ [∑(xi - x̄)² * ∑(yi - ȳ)²]
donde,
- xi es el valor i-ésimo de la variable x
- yi es el valor i-ésimo de la variable y
- x̄ es la media de la variable x
- ȳ es la media de la variable y
Ejemplos de correlación
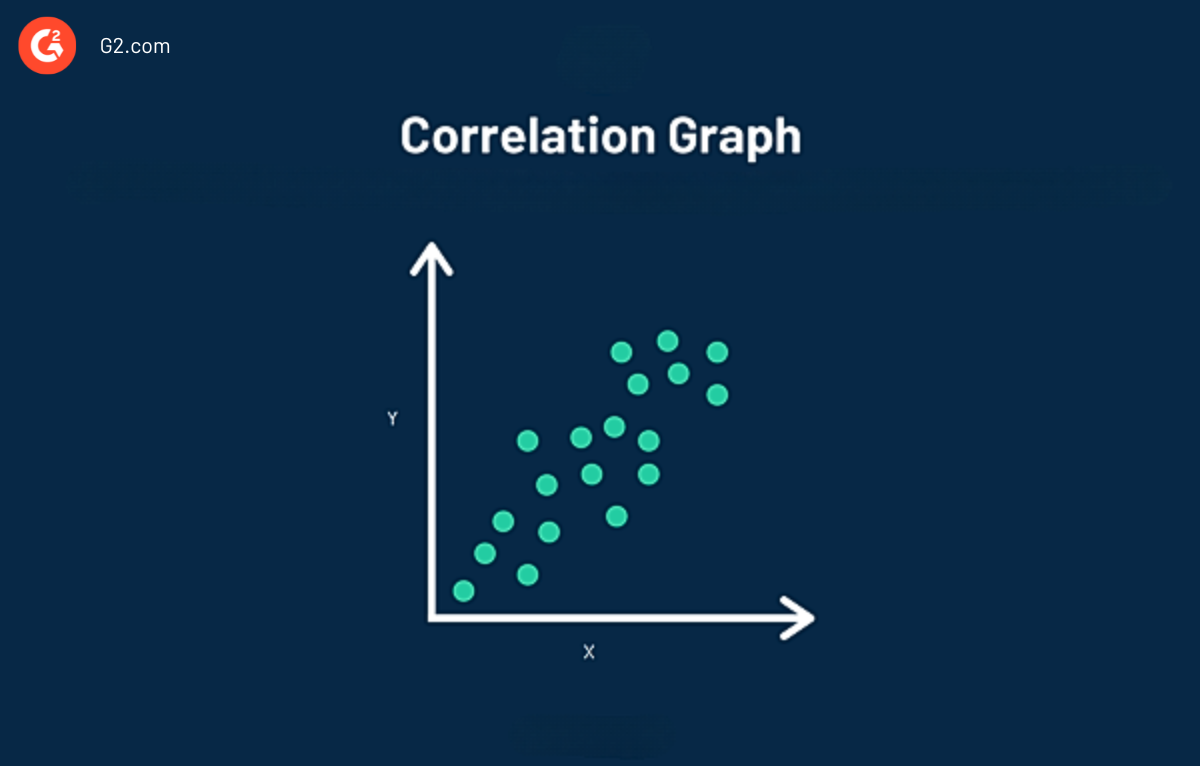
Un gráfico de correlación, también conocido como diagrama de dispersión, facilita ver la correlación entre dos variables visualmente. Los datos en un gráfico de correlación se representan mediante un solo punto. En el gráfico anterior, puedes observar que la correlación traza varios puntos de datos individuales.
Pensemos en la correlación como escenarios de la vida real. Además del ejemplo de precio y demanda mencionado anteriormente, desde una perspectiva financiera, cuanto más tiempo inviertas, más interés compuesto ganarás. O, contratar más vendedores resulta en mayores ingresos debido a que la empresa realiza más ventas.
Ahora veamos la correlación desde un punto de vista de marketing para ver la fuerza de una relación entre las dos variables. Por ejemplo, podría ser de interés para tu empresa ver si hay una relación predecible entre la venta de un producto y factores como el clima, la publicidad y los ingresos del consumidor.
¿Qué es la regresión?
Por otro lado, la regresión es cómo una variable afecta a otra o los cambios en una variable que desencadenan cambios en otra, esencialmente causa y efecto. Implica que el resultado depende de una o más variables.
Por ejemplo, mientras que la correlación puede definirse como la relación entre dos variables, la regresión es cómo se afectan entre sí. Un ejemplo de esto sería cómo un aumento en la lluvia causaría que varios cultivos crezcan, al igual que una sequía causaría que los cultivos se marchiten o no crezcan.
Cuando la variable dependiente aumenta mientras la variable independiente disminuye, o viceversa, se llama regresión negativa. Esto contrasta con una regresión positiva, donde tanto las variables dependientes como las independientes aumentan juntas.
Coeficiente de regresión
El análisis de regresión modela la relación entre una variable dependiente (el resultado) y una o más variables independientes (predictores). El coeficiente de regresión, o pendiente, cuantifica cuánto cambia la variable dependiente por cada cambio de una unidad en una variable independiente.
Análisis de regresión
El análisis de regresión ayuda a determinar la relación funcional entre dos variables (x e y) para que puedas estimar la variable desconocida y hacer proyecciones futuras sobre eventos y metas.
El objetivo principal del análisis de regresión es estimar los valores de una variable aleatoria (z) basándose en los valores de tus variables conocidas (o fijas) (x e y). El análisis de regresión lineal se considera la mejor línea de ajuste a través de los puntos de datos.
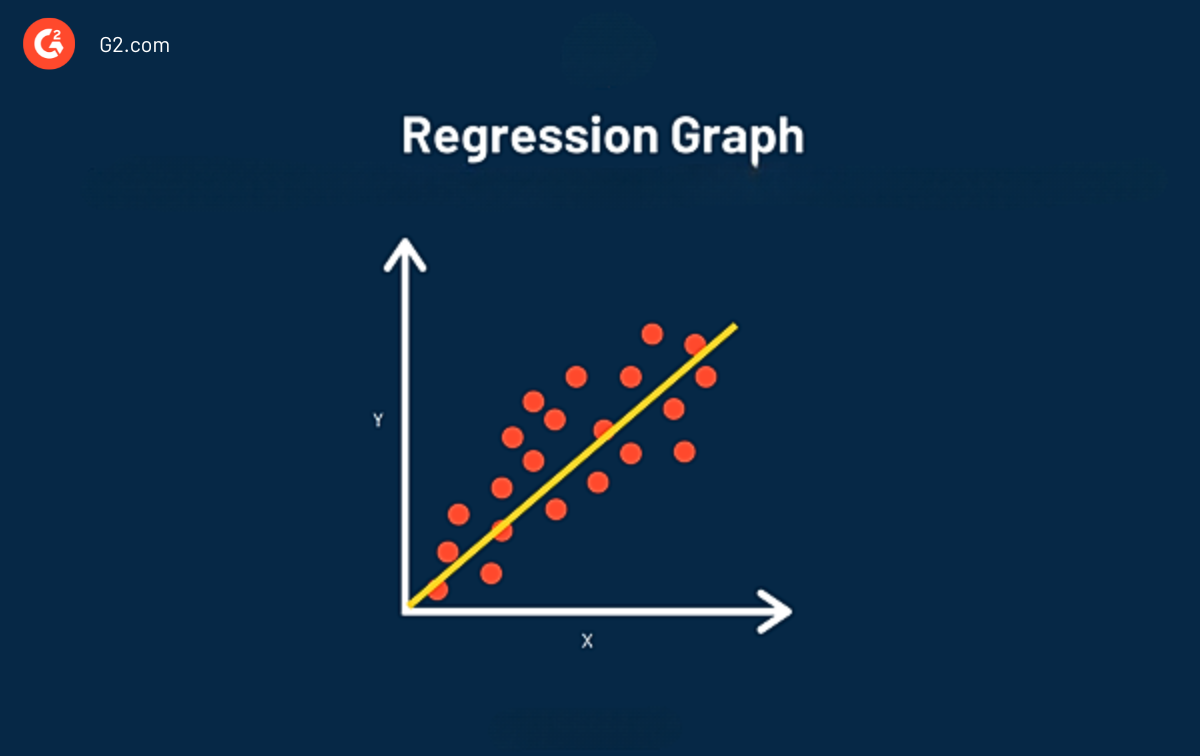
La principal ventaja de usar la regresión dentro de tu análisis es que proporciona una mirada detallada a tus datos (más detallada que solo la correlación) e incluye una ecuación que puede usarse para predecir y optimizar tus datos en el futuro.
Cuando se traza la línea usando regresión, podemos ver dos piezas de información:
Fórmula de regresión
a → se refiere a la intersección con el eje y, el valor de y cuando x = 0
b → se refiere a la pendiente, o subida sobre carrera
La fórmula de predicción utilizada para ver cómo podrían verse los datos en el futuro es:
y = a + b (x)
Ejemplos de regresión
Cuando se trata de usar la regresión, en G2 utilizamos la regresión para predecir ciertas tendencias, como cómo se espera que crezca nuestro tráfico en los próximos meses.
Una persona que usa la regresión es un SEO y Analista de Datos. Visualizar datos, analizarlos, identificar tendencias y predecir cómo podrían verse los datos en el futuro es una gran parte de su trabajo. Muchos equipos dependen de su trabajo para establecer metas de equipo y entender cómo podría verse nuestro tráfico en el futuro.
También usan las predicciones de modelos basados en regresión para establecer metas para métricas importantes de la empresa, como la adquisición de palabras clave. Dado que las predicciones se basan en datos históricos, esto le da a la empresa información sobre cómo está tendiendo actualmente en comparación con las tendencias de crecimiento pasadas.
Diferencia entre correlación y regresión
Hay algunas diferencias clave entre correlación y regresión que son importantes para entender los dos.
- Factores intercambiables: La regresión establece cómo x causa que y cambie, y los resultados cambiarán si x e y se intercambian. Con la correlación, x e y son variables que pueden intercambiarse y obtener el mismo resultado.
- Punto de datos único vs. ecuación: La correlación es una estadística única, o punto de datos, mientras que la regresión es toda la ecuación con todos los puntos de datos que están representados con una línea.
- Relación vs. efecto: La correlación muestra la relación entre las dos variables, mientras que la regresión nos permite ver cómo una afecta a la otra.
- Causa y efecto: Los datos mostrados con regresión establecen una causa y efecto. Cuando uno cambia, también lo hace el otro, y no siempre en la misma dirección. Con la correlación, las variables se mueven juntas.
Ahora es el momento de obtener noticias y entretenimiento SaaS-y con nuestro boletín de 5 minutos, G2 Tea, que presenta líderes inspiradores, opiniones audaces y predicciones atrevidas. ¡Suscríbete a continuación!
Similitudes entre correlación y regresión
Además de las diferencias, hay algunas similitudes clave entre correlación y regresión que pueden ayudarte a entender mejor tus datos.
- Ambos trabajan para cuantificar la dirección y la fuerza de la relación entre dos variables numéricas.
- Cada vez que la correlación es negativa, la pendiente de la regresión (línea dentro del gráfico) también será negativa.
- Cada vez que la correlación es positiva, la pendiente de la regresión (línea dentro del gráfico) será positiva.
Preguntas frecuentes sobre correlación y regresión
P. ¿Qué son la regresión y la correlación en estadística?
La correlación y la regresión son técnicas utilizadas para analizar la relación entre dos variables cuantitativas. Mientras que la correlación mide la fuerza de una relación lineal entre dos variables, la regresión en estadística mide cómo esas variables se afectan entre sí usando una ecuación.
P. ¿Cuál es una diferencia clave entre la regresión y la correlación?
La correlación determina la conexión o relación entre dos variables numéricas. La regresión se centra en cómo esa relación impactará a cada una de las variables con el tiempo.
P. ¿Debería usar correlación o regresión?
Usa correlación para conocer el grado de una relación entre dos variables. Pero si deseas analizar el efecto de cómo una variable independiente está asociada numéricamente con la variable dependiente, usa regresión.
P. ¿Puedes hacer correlación y regresión juntas?
Sí, el análisis de correlación y regresión puede realizarse juntos para medir un conjunto de datos y comprender la relación entre las variables.
Es más que causa y efecto.
Aunque se estudian juntos, está claro que hay diferencias y similitudes obvias entre correlación y regresión.
Cuando busques construir un modelo, una ecuación o predecir una respuesta clave, usa regresión. Si buscas resumir rápidamente la dirección y la fuerza de una relación, la correlación es tu mejor opción.
Para conceptualizar mejor tus datos, usa software de visualización de datos y rastrea tus métricas empresariales y KPIs en tiempo real.
Este artículo fue publicado originalmente en 2020. Ha sido actualizado con nueva información.

Mara Calvello
Mara Calvello is a Content and Communications Manager at G2. She received her Bachelor of Arts degree from Elmhurst College (now Elmhurst University). Mara writes content highlighting G2 newsroom events and customer marketing case studies, while also focusing on social media and communications for G2. She previously wrote content to support our G2 Tea newsletter, as well as categories on artificial intelligence, natural language understanding (NLU), AI code generation, synthetic data, and more. In her spare time, she's out exploring with her rescue dog Zeke or enjoying a good book.

