Was ist Regressionsanalyse?
Die Regressionsanalyse schätzt Beziehungen oder Verbindungen zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen. Sie bewertet die Stärke der Verbindung und das Potenzial für zukünftige Beziehungen.
Sie umfasst verschiedene Formen, darunter lineare, multiple lineare und nichtlineare Regression. Einfache lineare und multiple lineare Regression sind die gebräuchlichsten Modelle. Nichtlineare Regression hingegen wird angewendet, wenn es sich um komplexe Datensätze handelt, die eine nichtlineare Verbindung zwischen der abhängigen und den unabhängigen Variablen aufweisen.
Viele Fachleute ziehen es vor, die Regressionsanalyse zu verwenden, um genaue Geschäftsergebnisse vorherzusagen, wenn ein Geschäftsvorschlag von mehreren Faktoren abhängt. Die meisten Führungskräfte wenden sich an statistische Analysesoftware, um diese Bewertungen durchzuführen.
Arten der Regressionsanalyse
Die Regressionsanalysetechnik und die Auswahl des Ansatzes hängen von mehreren Faktoren ab, wie der Art der abhängigen Variablen und der Anzahl der unabhängigen Variablen. Nachfolgend sind einige gängige Arten der Regressionsanalyse aufgeführt.
- Einfache lineare Regressionsanalyse wird verwendet, um den Wert einer abhängigen Variablen basierend auf dem bekannten Wert einer unabhängigen Variablen vorherzusagen. Die Methode passt eine gerade Linie an, die es ermöglicht, die Beziehung zwischen den beiden Variablen zu definieren, indem die Koeffizienten in der linearen Gleichung geschätzt werden.
- Multiple Regressionsanalyse beschreibt eine Antwortvariable mit Hilfe mehrerer Prädiktorvariablen, wenn die Verbindungen zwischen den Daten komplexer sind. Dieser Ansatz funktioniert am besten, wenn starke Korrelationen zwischen den unabhängigen Variablen die abhängige Variable beeinflussen können.
- Gewöhnliche kleinste Quadrate Regression ist eine Methode, die unbekannte Parameter in einem Modell schätzt. Sie berechnet den Koeffizienten einer linearen Regressionsgleichung, indem die Summe der quadrierten Fehler zwischen den tatsächlichen und vorhergesagten Werten, die eine gerade Linie darstellt, verringert wird.
- Polynomiale Regression, eine Form der multiplen linearen Regression, kommt zum Einsatz, wenn die Beziehung zwischen den Datenpunkten nichtlinear ist. Sie bestimmt die kurvilineare Beziehung zwischen unabhängigen und abhängigen Variablen.
- Logistische Regression modelliert die Wahrscheinlichkeit der abhängigen Variablen basierend auf unabhängigen Variablen. Sie wird verwendet, wenn die abhängige Variable einen von einer begrenzten Menge binärer Werte (0 und 1) annehmen kann, was sie für die Analyse binärer Daten geeignet macht.
- Bayessche Regression wird angewendet, wenn Datensätze begrenzt oder schlecht verteilt sind. Wenn Daten nicht verfügbar sind, verwendet sie eine Wahrscheinlichkeitsverteilung, um das Ergebnis abzuleiten, anstatt Punkteschätzungen.
- Quantilregression schätzt spezifische Perzentile oder Quantile einer Antwortvariablen, anstatt sich ausschließlich auf den bedingten Mittelwert zu konzentrieren, wie in der linearen Regression. Sie widersteht dem Einfluss von Ausreißern und ist nicht auf Annahmen angewiesen.
- Ridge-Regression ist eine Regularisierungstechnik, die Multikollinearität unter den unabhängigen Variablen mindert oder wenn die Anzahl der unabhängigen Variablen die Anzahl der Beobachtungen übersteigt. Multikollinearität ist ein statistisches Konzept, bei dem mehrere unabhängige Variablen in einem Modell korreliert sind.
Vorteile der Regressionsanalyse
Die Nutzung der Regressionsanalyse zur Bewertung der Auswirkungen von Variablenänderungen bietet Unternehmen mehrere Vorteile.
- Datengetriebene Entscheidungen treffen. Bei der Planung für die Zukunft verlassen sich Unternehmen auf die Regressionsanalyse, um festzustellen, welche Variablen die Ergebnisse signifikant beeinflussen.
- Erkennen von Verbesserungsmöglichkeiten. Unternehmen können beobachten, wie die Erhöhung der Anzahl der Personen in einem Projekt das Umsatzwachstum beeinflusst. Die Regressionsanalyse zeigt Beziehungen zwischen Variablen auf und befähigt Unternehmen, Verbesserungsmöglichkeiten zu identifizieren.
- Optimierung von Geschäftsprozessen. Unternehmen nutzen die Regressionsanalyse, um die betriebliche Effizienz zu steigern. Zum Beispiel helfen Verbrauchererhebungen vor der Einführung einer neuen Produktlinie, zu verstehen, wie verschiedene Faktoren die Produktion beeinflussen.
Wie man Regressionsanalyse durchführt
Die Durchführung einer linearen Regression umfasst mehrere wichtige Schritte, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu berechnen.
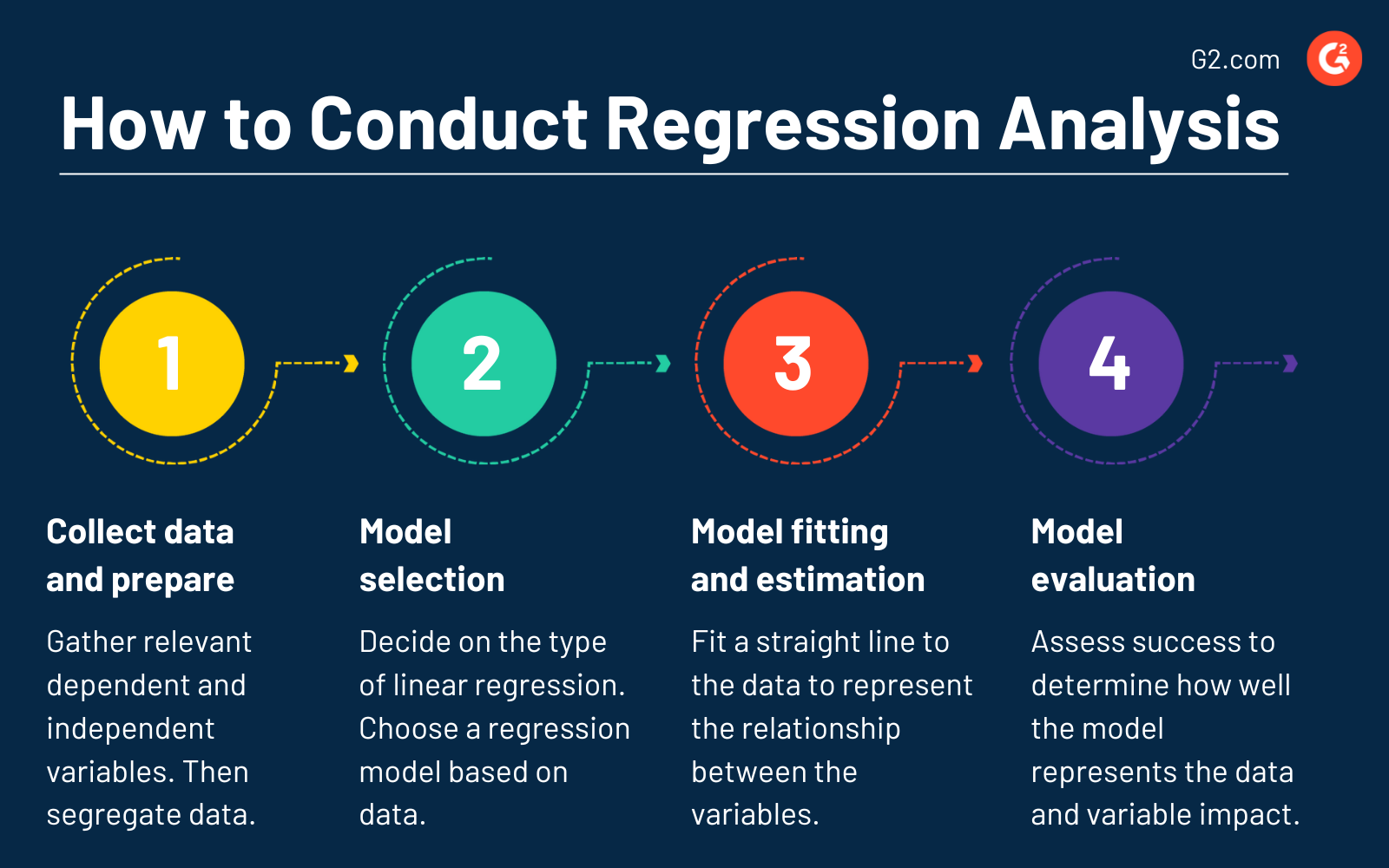
Hier sind die Hauptpunkte, die zu beachten sind:
- Datensammlung und -vorbereitung. Sammeln Sie relevante abhängige und unabhängige Variablen. Stellen Sie sicher, dass keine fehlenden Werte vorhanden sind, und überprüfen Sie auf Ausreißer, die die Analyseergebnisse beeinflussen könnten. Teilen Sie die Daten in Trainings- und Testsets auf, um die Leistung des Modells zu bewerten.
- Modellauswahl. Entscheiden Sie sich für die Art der linearen Regression. Wählen Sie das geeignete Regressionsmodell basierend auf den Datenmerkmalen aus.
- Modellanpassung und Koeffizientenschätzung. Bei der einfachen linearen Regression passen Sie eine gerade Linie an die Daten an, die die Beziehung zwischen der abhängigen und den unabhängigen Variablen am besten darstellt. Schätzen Sie im Gegensatz dazu die Koeffizienten der linearen Gleichung, um den Einfluss der unabhängigen Variablen auf die abhängigen Variablen bei der multiplen linearen Regression zu bestimmen.
- Modellevaluation. Bewerten Sie den Erfolg, um festzustellen, wie gut das Modell die Daten repräsentiert. Analysieren Sie die Signifikanz der Regressionskoeffizienten, um den Einfluss jeder unabhängigen Variablen auf die abhängige Variable zu verstehen.
Beste Praktiken der Regressionsanalyse
Nachfolgend sind einige wesentliche Best Practices aufgeführt, um sicherzustellen, dass Vorhersagen und Ergebnisse den tatsächlichen Werten nahekommen.
- Halten Sie Testsuiten aktuell. Stellen Sie sicher, dass die Funktionalität alter Funktionen mit neuen Upgrades überprüft wird.
- Nutzen Sie ein Regressionstest-Framework. Verwenden Sie Regressionstest-Frameworks, um Wartungsaufwände zu optimieren.
- Passen Sie Testdesigns an. Dies sollte von den Bedürfnissen der Entwickler und Tester bestimmt werden.
- Implementieren Sie automatisiertes Regressionstesten. Sparen Sie Ressourcen und beschleunigen Sie die Lieferung durch automatisiertes Regressionstesten.
- Identifizieren Sie Fehler vor der Bereitstellung. Automatisiertes Regressionstesten hilft, Fehler vor der Bereitstellungsfrist zu erkennen.
- Skalieren Sie mit cloudbasierter Testinfrastruktur. Da Anwendungen komplexer werden, stellen Sie sicher, dass die Testinfrastruktur skalieren kann, um die wachsende Anzahl zu bewältigen.
Regressionsanalyse vs. Korrelationsanalyse
Regressionsanalyse ist eine prädiktive Modellierungstechnik, die verwendet wird, um die Beziehung zwischen einer Zielvariablen und unabhängigen Variablen in einem Datensatz zu untersuchen. Verschiedene Regressionsanalysetechniken werden basierend darauf eingesetzt, ob die Beziehung zwischen der Ziel- und den unabhängigen Variablen linear oder nichtlinear ist und wenn die Zielvariable kontinuierliche Werte umfasst.
Korrelationsanalyse misst die Beziehung zwischen zwei Variablen, anstatt zu bewerten, wie zwei numerische Variablen einander beeinflussen.
Erfahren Sie mehr über den Unterschied zwischen Regression und Korrelation und verstehen Sie, wann welche zu verwenden ist.

Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.


















